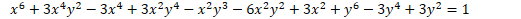Discussion Overview
The discussion revolves around the concept of rewriting an equation in accordance with PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction). Participants explore the implications of PEMDAS on the arrangement of terms in an equation, the purpose of such rearrangement, and the relevance of online calculators for this task.
Discussion Character
- Exploratory
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant expresses a desire to rewrite an equation according to PEMDAS but does not clarify the intended outcome or purpose.
- Another participant questions the need for rewriting in terms of PEMDAS and suggests that the original goal may be related to graphing the equation instead.
- There is a discussion about the misunderstanding of PEMDAS, with one participant asserting that changing the order of terms is unrelated to the order of operations defined by PEMDAS.
- A later reply introduces the concept of lexicographic order as an alternative way to arrange terms, referencing the Buchberger algorithm and suggesting that implementing such an order could be simpler than using an online calculator.
- Participants discuss the equivalence of different equations under the rules of PEMDAS, noting that the commutative property of addition allows for rearranging terms without changing the equation's meaning.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the purpose of rewriting the equation or the relevance of PEMDAS to the task. There are competing views on how to approach the arrangement of terms and the utility of online calculators.
Contextual Notes
Some participants express confusion regarding the distinction between rearranging terms and applying PEMDAS, indicating a need for clearer definitions and understanding of the concepts involved.