Finding parametric representation of a surface

[uzman1243]

Homework Statement

I am trying to find parametric representation of the right surface of a sphere which was cut along the line y=5.
x^2 + y^2 + z^2 = 36

Homework Equations

The Attempt at a Solution

x^2 + y^2 + z^2 = 36

This is an equation of a sphere with radius given by:

r^2 = 36
r=6

x= r cos(theta)sin(phi)
y= r sin(theta)sin(phi)
z= r cos(theta)

sub x,y,z into original equation to get function with theta,phi as parameters.

Have is the correct way to start? if so, how do I proceed?

 

[Mark44]

Homework Statement

I am trying to find parametric representation of the right surface of a sphere which was cut along the line y=5.

In three dimensions, y = 5 is a plane. It is 5 units to the right of the x-z plane.

x^2 + y^2 + z^2 = 36

Homework Equations

The Attempt at a Solution

x^2 + y^2 + z^2 = 36

This is an equation of a sphere with radius given by:

r^2 = 36
r=6

x= r cos(theta)sin(phi)
y= r sin(theta)sin(phi)
z= r cos(theta)

sub x,y,z into original equation to get function with theta,phi as parameters.

Have is the correct way to start? if so, how do I proceed?

I'm not sure how much help this will be, but the y coordinate lies between 5 and 6, and the x and z values range between $-\sqrt{11}$ and $\sqrt{11}$, depending on the particular point on the portion of the sphere.

 

[LCKurtz]

Homework Statement

I am trying to find parametric representation of the right surface of a sphere which was cut along the line y=5.
x^2 + y^2 + z^2 = 36

Homework Equations

The Attempt at a Solution

x^2 + y^2 + z^2 = 36

This is an equation of a sphere with radius given by:

r^2 = 36
r=6

That is the equation of the sphere in spherical coordinates, except it's best to use the standard $\rho$ instead of $r$ for the radius. So you have $\rho = 6$, which I have put in below for you:

x= 6cos(theta)sin(phi)
y= 6sin(theta)sin(phi)
z= 6cos(theta)

and you just need to know the ranges for $\phi$ and $\theta$ to get the portion of the sphere to the right of the plane $y=5$.

Draw the circle and straight line in the $yz$ plane giving the trace of these two surfaces. You should be able to figure out from that picture what values of $\phi$ give the portion of the circle to the right of the plane. Same idea in the $xy$ plane for $\theta$.

 

[uzman1243]

Draw the circle and straight line in the $yz$ plane giving the trace of these two surfaces. You should be able to figure out from that picture what values of $\phi$ give the portion of the circle to the right of the plane. Same idea in the $xy$ plane for $\theta$.

Can you explain this part a little more?

 

[Mark44]

I'm not sure what LCKurtz meant by his reply, since you're dealing with a sphere rather than a circle. The plane y = 5 slices a piece of the sphere, and intersects the sphere to form a circle.

 

[uzman1243]

I'm not sure what LCKurtz meant by his reply, since you're dealing with a sphere rather than a circle. The plane y = 5 slices a piece of the sphere, and intersects the sphere to form a circle.

So how do I proceed?

 

[Mark44]

Follow what LCKurtz said:

you just need to know the ranges for ϕ and θ to get the portion of the sphere to the right of the plane y=5.

 

[uzman1243]

Follow what LCKurtz said:

Yes. I don't understand what that means

 

[Mark44]

Have you drawn a sketch of the region sliced off the sphere?
The plane y = 5 intersects the sphere in a circle whose center is at (0, 5, 0) and whose radius is $\sqrt{11}$. What are the coordinates of the highest and lowest points on this circle? That should give you an idea of the range of $\phi$.
What are the coordinates of the points that are furthest in the direction of the x-axis, and the furthest in the direction of the negative x-axis? These points should give you the range of $\theta$. I believe that's what LCKurtz was talking about.

 

[LCKurtz]

Here's what I mean by the trace of the surfaces in the zy plane. (Standard usage of trace):

You should be able to figure out the two values of $\phi$ from the two arcs. A similar trace in the xy plane should help you figure out the range for $\theta$. Just don't expect the angles to be one of the "standard" angles like $\pi/6$.

[Edit, added]: It may be a bit more complicated in that the limits of $\phi$ may depend on the value of $\theta$. Actually, that does happen. I will add to this tomorrow.

 

[LCKurtz]

OK, I think we need to do a restart on this problem. I will begin with a new 3D picture of just the first octant portion of this problem.

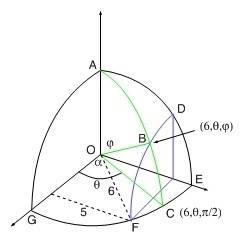
I have indicated a general $\theta$ and the green lines are in the plane generated by that $\theta$ as $\phi$ and $\rho$ vary. Note that as $\phi$ varies from $0$ to $\pi /2$ the end of the $\rho=6$ line sweeps along the green arc ABC. Point B is the place where $\phi$ begins to hit the part of the sphere to the right of $y=5$. The plane $y=5$ is outlined with the purple lines. Notice that if $\theta$ were $\pi / 2$ then $\phi$ would only sweep out the arc AD before hitting the plane $y=5$. That is a shorter arc than AB so the lowest value of $\phi$ to hit the plane depends on $\theta$. To get the relation between $\phi$ and $\theta$, look at the point $B =(6,\theta,\phi)$. That point lies on the plane $y=5$. The spherical coordinate equation for $y$ in general is $y=\rho\sin\phi\sin\theta$. Applying that to this point gives $5 = 6\sin\phi\sin\theta$ so $\sin\phi =\frac 5 {6\sin\theta}$. So, finally, the dependence of $\phi$ on $\theta$ is$$
\phi = \arcsin\left(\frac 5 {6\sin\theta}\right)$$So, in this picture, depending on what $\theta$ is, we would have$$
\arcsin\left(\frac 5 {6\sin\theta}\right)\le \phi \le \frac \pi 2$$Of course, for the full problem, $\phi$ wouldn't stop at $\pi /2$.

In the picture, $\alpha$, which is angle GOF in the xy plane, would be the min value of $\theta$ and its max would be $\pi/2$, but it wouldn't stop there for the non-first octant part. I have deliberately not done more than the first octant to leave the OP something to do, yet I pretty much couldn't do less and explain the problem clearly.

BUT, and this is the real lesson here, while this is a great exercise for doing complicated limits and gives a perfectly good parameterization, it is NOT the best way to work this problem.

To see this, think about how much simpler this problem would have been if it had asked for the parameterization of the part of the sphere above the plane $z=5$ instead of to the right of the plane $y=5$. If you set that problem up in spherical coordinates, the $\theta$ and $\phi$ limits are easy, constant, and don't depend on each other. So think about solving that problem. Once you have that solved, you only have to rename the variables so instead of using the $z$ axis for the azimuth angle, use the $y$ axis.