Finding the transformation of a matrix

[Redwaves]

Homework Statement

Finding the transformation of a matrix

Relevant Equations

$\begin{bmatrix} cos \theta & sin \theta \\ sin \theta & -cos \theta \end{bmatrix}$

I have the matrix above and I have to find which transformation is that.
$\begin{bmatrix} cos \theta & sin \theta \\ sin \theta & -cos \theta \end{bmatrix}$

For a vector $\vec{v}$

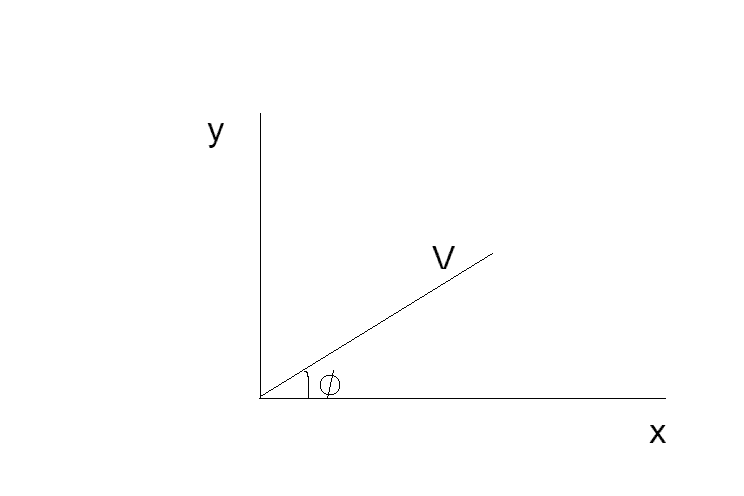
$v_x' = v_x cos \theta + v_y sin \theta$
$v_y' = v_x sin \theta - v_y cos \theta$

If $\phi$ is the angle between x-axis and the vector $\vec{v}$, then $v_x = r cos \theta$ and $v_y = r sin \theta$

Thus,
$v_x = r cos \phi cos \theta + r sin\phi sin\theta$ = $r cos(\phi - \theta)$
$v_y = r cos \phi sin \theta - r sin\phi cos\theta$ = - $r sin(\phi - \theta)$

From that, the transformation seems to be an rotation of $\phi - \theta$ clockwise and then a reflection over the x axis. Is this correct?

 

[PeroK]

Where did $\phi$ come from?

 

[Redwaves]

Where did $\phi$ come from?

Between x and $\vec{v}$

 

[PeroK]

Between x and $\vec{v}$

What has that to do with a matrix that is a function of $\theta$?

 

[Redwaves]

What has that to do with a matrix that is a function of $\theta$?

$\vec{v}$ is an arbitrary vector to help me figure out what the matrix does.

 

[PeroK]

$\vec{v}$ is an arbitrary vector to help me figure out what the matrix does.

I understand that, but what the matrix does can only depend on $\theta$ and not on some other angle. I'm struggling to see how another angle could be involved in the general matrix operation.

 

[PeroK]

PS if you know how to write the rotation and reflection matrices, then you can check your answer. Do you know how?

 

[Redwaves]

PS if you know how to write the rotation and reflection matrices, then you can check your answer. Do you know how?

I watched youtube videos and they use the same way as I did to find the rotation matrix. A vector $\vec{v}$ and an angle $\phi$ between x and $\vec{v}$. Otherwise, I don't know.

 

[PeroK]

I watched youtube videos and they use the same way as I did to find the rotation matrix. A vector $\vec{v}$ and an angle $\phi$ between x and $\vec{v}$. Otherwise, I don't know.

Okay, let's check whether the matrix is a rotation by $\phi - \theta$ clockwise followed by a reflection in the $x$ axis. How would you check that?

Hint: you could do an Internet search for "rotation matrix" and "reflection matrix".

 

[Redwaves]

Hint: you could do an Internet search for "rotation matrix" and "reflection matrix".

I did, but this matrix is neither a rotation or a reflection matrix.

 

[PeroK]

I did, but this matrix is neither a rotation or a reflection matrix.

I know! Maybe you need to think about matrix operations?

 

[PeroK]

PS why don't we use the vector $(1, 2)$ as an example? Calculate what your matrix does to that.

And, we could set $\theta = \frac{\pi}{4}$ perhaps. Just to check what happens to a given vector for a simple value of $\theta$.

That should let you check your answer.

 

[Redwaves]

PS why don't we use the vector $(1, 2)$ as an example? Calculate what your matrix does to that.

And, we could set $\theta = \frac{\pi}{4}$ perhaps. Just to check what happens to a given vector for a simple value of $\theta$.

That should let you check your answer.

$x' = \frac{3\sqrt{2}}{2}$
$y' = -\frac{\sqrt{2}}{2}$
It seems to be the same transformation as I said, no?

 

[PeroK]

$x' = \frac{3\sqrt{2}}{2}$
$y' = -\frac{\sqrt{2}}{2}$
It seems to be the same transformation as I said, no?

Where's $\phi$?

 

[PeroK]

$x' = \frac{3\sqrt{2}}{2}$
$y' = -\frac{\sqrt{2}}{2}$
It seems to be the same transformation as I said, no?

PS No. It's not a rotation followed by a reflection.

 

[Redwaves]

I mean, if you draw the new vector using both way the new vector is in the same position.

 

[PeroK]

I mean, if you draw the new vector using both way the new vector is in the same position.

That's not what I get. What about looking at the basis vectors $(1,0)$ and $(0,1)$?

When you say "a clockwise rotation of $\phi - \theta$", what does that mean?

 

[Redwaves]

When you say "a clockwise rotation of $\phi - \theta$", what does that mean?

$\theta$ is the angle between $\vec{v}'$ and the x axis.
Thus. $\phi - \theta$ is the angle between $\vec{v}$ and $\vec{v}'$.
$\vec{v}'$ is closer to the x axis.

Is it clear?

 

[PeroK]

$\theta$ is the angle between $\vec{v}'$ and the x axis.
Thus. $\phi - \theta$ is the angle between $\vec{v}$ and $\vec{v}'$.
$\vec{v}'$ is closer to the x axis.

Is it clear?

This is not right. The matrix you have is a reflection in the $x$ axis followed by a rotation by $\theta$. By convention rotations are anti-clockwise.

Alternatively, it's a rotation of $-\theta$ followed by reflection in the $x$ axis.

There's no $\phi$ involved, regardless of what you've seen on Youtube.

The other thing you are missing is that you can use matrix multiplication to generate a rotation followed by a reflection or vice versa.

That's how you could have checked your answer.

 

[Redwaves]

In this case how can I find the rotation matrix and the reflection? I was able to find both matrices using my way. Otherwise, I don't see how.

What's $\theta$? the angle between x and v ?

 

[PeroK]

In this case how can I find the rotation matrix and the reflection? I was able to find both matrices using my way. Otherwise, I don't see how.

The first thing I would do is check what it does to the basis vectors:

$(1, 0) \rightarrow (\cos \theta, \sin \theta)$

$(0, 1) \rightarrow (\sin \theta, -\cos \theta)$

You can see from that that you have to do the reflection in the $x$ axis first.

Then I would check that $R_{\theta} R_x$ equals the matrix you were given. Note the order in the matrix multiplication. This is because you want the reflection first:$$R_{\theta} R_x v$$

 

[Redwaves]

What's $R$ ?
How can I prove the reflection and the rotation without using any specific vector.

Is $\theta$ the angle between x and v ?

How can I prove the rotation matrix without using $\phi$, that is what I used.

Everything seems less clear.

 

[Redwaves]

I think what you say is exactly what I say in a different way and that's what confuse me.

$v_x = r cos (\phi - \theta)$
$v_y = - r sin (\phi - \theta)$
is a rotation of $-\theta$ from the initial angle like you say and a reflection in the x axis.

 

[PeroK]

What's $R$ ?
How can I prove the reflection and the rotation without using any specific vector.

Is $\theta$ the angle between x and v ?

How can I prove the rotation matrix without using $\phi$, that is what I used.

Everything seems less clear.

$R_{\theta}$ is the matrix representing a (counterclockwise) rotation by $\theta$. $R_x$ is the matrix representing reflection in the $x$ axis.

You can prove it by matrix multiplication. Once you have the matrix equation, there is no need to consider vectors, either specific or general.

There's no need to involve $\phi$. The video you saw has confused you. It's possible to represent a vector using a polar angle $\phi$, but that is ultimately irrelevant to the matrix itself.

 

[Redwaves]

You can prove it by matrix multiplication. Once you have the matrix equation, there is no need to consider vectors, either specific or general.

This is a lot of trial and error, no?
Assuming I know the transformations matrix and I don't have to prove them before using them.

 

[PeroK]

This is a lot of trial and error, no?
Assuming I know the transformations matrix.

No, because by checking the action on the basis vectors first you should be able to see what the matrix does. Checking the matrix multiplication just confirms that.

 

[Redwaves]

Is the reflection matrix
$\begin{bmatrix} cos 2\theta & sin 2\theta \\ sin 2 \theta & - cos 2\theta \end{bmatrix}$

Because I don't get the starting matrix.

https://en.wikipedia.org/wiki/Rotations_and_reflections_in_two_dimensions

 

[PeroK]

Is the reflection matrix
$\begin{bmatrix} cos 2\theta & sin 2\theta \\ sin 2 \theta & - cos 2\theta \end{bmatrix}$

Because I don't get the starting matrix.

The reflection matrix is:
$$\begin{bmatrix}
1 & 0 \\
0 & -1
\end{bmatrix}$$
You can check that matrix maps $(x, y)$ to $(x, -y)$

There's no $\theta$ in a reflection in the $x$ axis.

 

[Redwaves]

I see,
so it's a reflection followed by a rotation anticlockwise by $\theta$ why the reflection first if this is $R_\theta R_x$

 

[PeroK]

I see,
so it's a reflection followed by a rotation anticlockwise by $\theta$ why the reflection first if this is $R_\theta R_x$

That's the way matrices acting on vectors work: $$Mv = R_\theta (R_xv)$$That means you first reflect $v$, then rotate the resultant vector.

 

[Redwaves]

I see, I didn't know that.
I guess I understand. I'll practice to make sure I understand properly.
Thank you

 

[FactChecker]

From that, the transformation seems to be an rotation of $\phi - \theta$ clockwise and then a reflection over the x axis. Is this correct?

Yes, you are correct. It can be represented by
$\begin{pmatrix} \cos(\theta) & \sin(\theta) \\ \sin(\theta) & -\cos(\theta) \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} \cos(-\theta) & -\sin(-\theta) \\ \sin(-\theta) & \cos(-\theta) \end{pmatrix}$
That is a rotation of angle $\theta$ in the clockwise direction followed by a reflection across the X-axis.