JJBladester
Gold Member
- 281
- 2
What is the voltage across R2? You should convert the 4 V source and resistor into a current source as your first step.
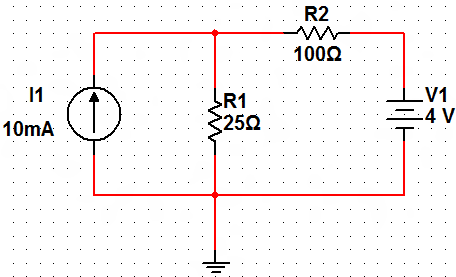
The first thing I did is create a second current source out of the 4 V voltage source and the series resistor R2. I called it I_2.
I_2 = E/R_2 = 4V/100Ω = 40 mA
This gives us:
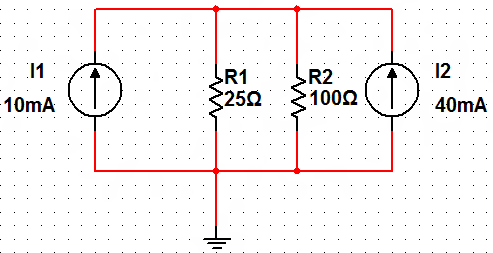
We can combine the parallel current sources I_1 and I_2:
I = I_1 + I_2 = 10 mA + 40 mA = 50 mA
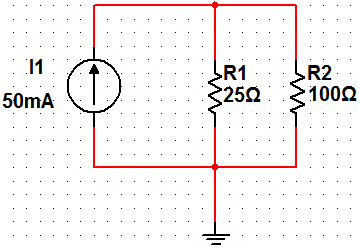
By the current divider rule,
I_R2 = (R_T*I)/R2 = (20Ω*50mA)/100Ω = 10 mA
V_R2 = I_R2*R2 = 10mA * 100Ω = 1 V
However, when I run a simulation of the original circuit using MultiSim, I get 3 V through R2. Where am I going wrong?
The first thing I did is create a second current source out of the 4 V voltage source and the series resistor R2. I called it I_2.
I_2 = E/R_2 = 4V/100Ω = 40 mA
This gives us:
We can combine the parallel current sources I_1 and I_2:
I = I_1 + I_2 = 10 mA + 40 mA = 50 mA
By the current divider rule,
I_R2 = (R_T*I)/R2 = (20Ω*50mA)/100Ω = 10 mA
V_R2 = I_R2*R2 = 10mA * 100Ω = 1 V
However, when I run a simulation of the original circuit using MultiSim, I get 3 V through R2. Where am I going wrong?