Finding Slope of Tangent Line: How-To Guide

Click For Summary
SUMMARY

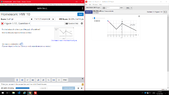
The discussion focuses on finding the slope of tangent lines for various segments of a piecewise linear function. Participants clarify that only straight lines possess a constant slope, while curves exhibit varying slopes at different points. The specific segments analyzed include three straight lines: from (-5, 5) to (-2, 2), from (-2, 2) to (0, 4), and from (0, 4) to (4, 2). The slope calculations for these segments are essential for understanding the concept of slope in both linear and non-linear contexts.

PREREQUISITES
  • Understanding of linear equations and slope calculation
  • Familiarity with piecewise functions
  • Basic knowledge of coordinate geometry
  • Ability to interpret graphical representations of functions
NEXT STEPS
  • Study the concept of slope in linear functions
  • Learn how to calculate slopes of piecewise linear functions
  • Explore the differences between tangent lines and secant lines
  • Investigate the application of derivatives in finding slopes of curves
USEFUL FOR

Students learning calculus, mathematics educators, and anyone interested in understanding the principles of slope in both linear and non-linear functions.

Teh
Messages
47
Reaction score
0
View attachment 6115
My professor shown us in class how to find the slope but I still don't understand
 

Attachments

  • mathhwk1.png
    mathhwk1.png
    60.1 KB · Views: 110
Physics news on Phys.org
Find which slope? Surely your professor, when showing how to find slope explained that only straight lines have a single slope. Other curves, including "broken line curves" like this, have different slopes at different points. Here there are three different straight lines, one from (-5, 5) to (-2, 2), another from (-2, 2) to (0, 4), and the third from (0, 4) to (4, 2). What is the slope of each of those?
 

Similar threads

High School Why does the Limit Process give an Exact Slope?
  • · Replies 53 ·
2
Replies
53
Views
6K
High School How to Find the Intersection of a Logarithmic Curve and a Tangent Line?
  • · Replies 14 ·
Replies
14
Views
2K
MHB Slope of Tangent line to Polar curve
  • · Replies 2 ·
Replies
2
Views
2K
MHB Calculus III: Proving Tangent Line = 1 for Every Point on Curve
  • · Replies 1 ·
Replies
1
Views
2K
MHB -apc.4.1.2 Find the slope at x=4
  • · Replies 7 ·
Replies
7
Views
2K
MHB 210 AP Calculus Exam problem tangent line to curve
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Calc 1 practice exam question -- finding the y intercept of the tangent line
  • · Replies 6 ·
Replies
6
Views
2K
MHB Equation of the Tangent Line? (Derivatives)
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Question about gradient, tangent plane and normal line
  • · Replies 1 ·
Replies
1
Views
2K
High School Nature of Limits: Learn Calculus Basics w/o Limits Distraction
  • · Replies 13 ·
Replies
13
Views
3K