Finding Tension and theta in a pulley system

[jalalapeno]

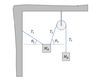
What I've attempted to do is resolve vertically and horizontally:
T₁sin(30)+T₂sinΘ+T₂=9g
T₂cosΘ=T₁cos30

After that... I'm completely stuck. Any help would be appreciated, I've spent so long on this I bet I'm just missing one simple thing.
Thanks in advance

 

[Orodruin]

T1sin(30)+T2sinΘ+T2=9g
T2cosΘ=T1cos30

What is your reasoning behind those equations? What are the systems you are drawing free-body-diagrams and considering equilibrium for? Note that the equilibrium means that each mass in the system is in equilibrium and you can consider them separately.

 

[jalalapeno]

What is your reasoning behind those equations? What are the systems you are drawing free-body-diagrams and considering equilibrium for? Note that the equilibrium means that each mass in the system is in equilibrium and you can consider them separately.

I got those equations by considering the system as a whole, resolving vertically and horizontally.
So you're saying T₂=5g?

 

[Orodruin]

I got those equations by considering the system as a whole, resolving vertically and horizontally.

"As a whole" really has no meaning. I suspect you mean "masses 1 and 2". The system "as a whole" would include the walls, ceiling, pulley, etc. Now, of course you can consider both masses together, but you can also consider them one at a time since each of them needs to be at equilibrium for the system to be at equilibrium. I suggest that you do this.

 

[jalalapeno]

"As a whole" really has no meaning. I suspect you mean "masses 1 and 2". The system "as a whole" would include the walls, ceiling, pulley, etc. Now, of course you can consider both masses together, but you can also consider them one at a time since each of them needs to be at equilibrium for the system to be at equilibrium. I suggest that you do this.

I just keep getting different answers. My latest answers are Θ=13.8 and Θ=73.7
From those it should be 73.7 because the angle should be larger than 30 (Θ₁ )
Can anyone also do it to double check? or just tell me I'm wrong haha

 

[Orodruin]

Please show the reasoning behind your results. It is the only way we can check them and look for where your logic fails.

 

[jalalapeno]

Please show the reasoning behind your results. It is the only way we can check them and look for where your logic fails.

Of course

Resolving Vertically for mass B gives: T₂ = 5g
Resolving Vertically for mass A gives: T₁sin(30) + T₂sinΘ = 4g
Subbing T₂ = 5g back: 1/2T₁ + 5gsinΘ = 4g
sin30 = 1/2
Resolving Horizontally for mass A gives: 5gcosΘ = T₁cos30
Rearranging for T₁ : T₁ = 5gcosΘ/cos(30)
Subbing T₁ into the 2nd formula gives: 5gsinΘ + (1/2)(5gcosΘ/cos(30))=4g
Making that a bit neater gives: sinΘ + √3/3cosΘ = 4/5
sinΘ - 4/5 = -(√3/3cosΘ)
Squaring the whole equation gives: sin²Θ - 8/5sinΘ + 16/25 =1/3cos²Θ
cos^Θ = 1 - sin²Θ

4/3sin²Θ - 8/5sinΘ +23/75 = 0
sinΘ = 0.96 and sinΘ = 0.24
Θ = 73.7° and Θ = 17.9°

 

[jalalapeno]

Might be a bit hard to follow apologies

 

[haruspex]

Which of your two solutions satisfies

sinΘ - 4/5 = -(√3/3cosΘ)

 

[jalalapeno]

Which of your two solutions satisfies

sinΘ = 73.7 satisfies sinΘ - 4/5 = -(√3/3cosΘ)
Thank you both for your help, really appreciate it!

 

[haruspex]

sinΘ = 73.7 satisfies sinΘ - 4/5 = -(√3/3cosΘ)

You mean θ=73.7°, but doesn't that make the two sides opposite signs?

 

[jalalapeno]

You mean θ=73.7°, but doesn't that make the two sides opposite signs?

It does, but I’ve decided to ignore that for now as this question has given me enough stress :D

 

[haruspex]

It does, but I’ve decided to ignore that for now as this question has given me enough stress :D

You would do better to take note of it. What about the other solution that came out of the quadratic?

the angle should be larger than 30

Why?

 

[jalalapeno]

You would do better to take note of it. What about the other solution that came out of the quadratic?
Why?

I have compared my results to others in the class and nobody really knows how to do it...

 

[Orodruin]

I have compared my results to others in the class and nobody really knows how to do it...

What does this have to do with the question haruspex asked? Or the solution to the problem for that matter?

 

[jalalapeno]

What does this have to do with the question haruspex asked? Or the solution to the problem for that matter?

That’s my bad
Using both results from the quadratic I do get an answer that works, and that is 13 degrees but I don’t know if that makes sense in a physical sense.

 

[Orodruin]

Then why do you not just check that the solution satisfies the original equilibrium equations that you wrote down?

 

[jalalapeno]

Then why do you not just check that the solution satisfies the original equilibrium equations that you wrote down?

I have, and one of the solutions satisfies the equation. The angle I have calculated isn’t 13.8 degrees. I am trying to work out if this makes sense in the real world.

 

[VKint]

I'm getting 13.85 degrees.

The thing you need to remember is that diagrams such as the one you uploaded do not necessarily reflect the problem's eventual solution. Even though the diagram is drawn so it appears that $\theta_2 > \theta_1$, there is no reason to assume that this is the case. This is a specific instance of a problem I've encountered many times--frequently, when I'm thinking about a complicated problem, I draw a diagram and begin to make assumptions and write equations based on it, only to realize later that I've inadvertently incorporated some of the "non-generic" features of the diagram into the math.

By the way, I always recommend writing your equations without using specific numbers at first, only substituting at the end of the problem. In this case it makes the solution much cleaner and easier to follow. Indeed, the equations for equilibrium are
$$M_A g = T_1 \sin (\theta_1) + T_2 \sin(\theta_2)$$ $$T_1 \cos(\theta_1) = T_2 \cos(\theta_2)$$ $$M_B g = T_2$$
Using the second equation to eliminate $T_1$ and the third to eliminate $T_2$, and rearranging a bit, gives
$$\frac{M_A}{M_B} = \tan(\theta_1) \cos(\theta_2) + \sin(\theta_2)$$
Now, there are various ways of solving this equation, but the clearest seems to be doing what the problem suggests--using this to generate a quadratic equation for $\tan(\theta_2)$. Let's clean up the notation a bit: Let $r = M_A / M_B$, $t = \tan(\theta_1)$, and $T = \tan(\theta_2)$. Divide both sides by $\cos(\theta_2)$ and square:
$$r^2 \left( \frac{1}{\cos^2(\theta_2)} \right) = t^2 + 2tT + T^2$$
Finally, use the identity $\cos^{-2}(\theta_2) = 1 + \tan(\theta_2)^2 = 1 + T^2$ to get (again after rearranging)
$$(1 - r^2) T^2 + 2tT + (t^2 - r^2) = 0$$ which is the promised quadratic equation. Solving it gives the two solutions $T \approx .246619$ and $T \approx -3.45412$, of which only the former is physical. Taking an inverse tangent gives $\theta_2 \approx 13.85$ degrees.

 

[jalalapeno]

I'm getting 13.85 degrees.

The thing you need to remember is that diagrams such as the one you uploaded do not necessarily reflect the problem's eventual solution. Even though the diagram is drawn so it appears that $\theta_2 > \theta_1$, there is no reason to assume that this is the case. This is a specific instance of a problem I've encountered many times--frequently, when I'm thinking about a complicated problem, I draw a diagram and begin to make assumptions and write equations based on it, only to realize later that I've inadvertently incorporated some of the "non-generic" features of the diagram into the math.

By the way, I always recommend writing your equations without using specific numbers at first, only substituting at the end of the problem. In this case it makes the solution much cleaner and easier to follow. Indeed, the equations for equilibrium are
$$M_A g = T_1 \sin (\theta_1) + T_2 \sin(\theta_2)$$ $$T_1 \cos(\theta_1) = T_2 \cos(\theta_2)$$ $$M_B g = T_2$$
Using the second equation to eliminate $T_1$ and the third to eliminate $T_2$, and rearranging a bit, gives
$$\frac{M_A}{M_B} = \tan(\theta_1) \cos(\theta_2) + \sin(\theta_2)$$
Now, there are various ways of solving this equation, but the clearest seems to be doing what the problem suggests--using this to generate a quadratic equation for $\tan(\theta_2)$. Let's clean up the notation a bit: Let $r = M_A / M_B$, $t = \tan(\theta_1)$, and $T = \tan(\theta_2)$. Divide both sides by $\cos(\theta_2)$ and square:
$$r^2 \left( \frac{1}{\cos^2(\theta_2)} \right) = t^2 + 2tT + T^2$$
Finally, use the identity $\cos^{-2}(\theta_2) = 1 + \tan(\theta_2)^2 = 1 + T^2$ to get (again after rearranging)
$$(1 - r^2) T^2 + 2tT + (t^2 - r^2) = 0$$ which is the promised quadratic equation. Solving it gives the two solutions $T \approx .246619$ and $T \approx -3.45412$, of which only the former is physical. Taking an inverse tangent gives $\theta_2 \approx 13.85$ degrees.

Thank you for the tips and very clear explanation. I think the way you have done it by not substituting in numbers until the end is the best way to do as to not get confused or make any mistakes.
Really appreciate your help :D

 

[haruspex]

Thank you for the tips and very clear explanation. I think the way you have done it by not substituting in numbers until the end is the best way to do as to not get confused or make any mistakes.
Really appreciate your help :D

Yes, I always encourage working purely symbolically until the end. It has many advantages.
It might help to understand why the non-physical solution occurs. In order to obtain the quadratic equation you had to square

sinΘ - 4/5 = -(√3/3cosΘ)

But you would have got the same squared equation had you started with
sinΘ - 4/5 = +(√3/3cosΘ)
So this creates an ambiguity in the squared form. To figure out which is the right answer you have to substitute the two answers in the unsquared equation.