Finding the angle that a string makes with a wall and its tension

[JohnnyLaws]

Homework Statement

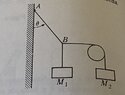
We have two bodies (first one has 300Kg and another one has400Kg) in equilibrium connected by a massless string and there's no friction. The first one is held by a thread that makes an angle theta with the wall as we will see in image. The second one is held by same thread that is held by a pulley. I need to calculate angle theta and the Tension that string makes between points A and B (points that We Will see in image).

Relevant Equations

To define the equations I used (I'm not sure if they are correct), I need to explain force vectors. It's probably better to start by looking at the image before we delve into the equations.

T1 = is first Tension wich is produzed in points A and B.
T2 = is Tension that body 2 creates
T3 = is Tension that body creates
W1 = weight of body 1
W2 = weight of body 2



T1cos(theta)+T3-W1 = 0
That first equation is refering to body 1
T1cos(theta)+T2-w2 = 0
That second equation is refering to body 2
-T1sin(theta)-T2+T3= 0
That thirth equation is refering to body horizontal forces of the string


I'm pretty sure those equations are wrong because I have 3 variables for 4 equations

For a better understanding of this exercise here is the image illustrating the scenario described in the statement:
View attachment 330011
So to solve this exercise I began by drawing a forces diagram:

I believe I have explained everything in the "Relevant equations" section. What am I doing wrong? The book that I'm reading doesn't have any solutions.

 

[JohnnyLaws]

I don't know why the image of the exercise doesn't appear. Here it is:

 

[kuruman]

Your force diagram has too many forces in places. For example, in the horizontal piece of rope you can't have T2 pointing to the left and T3 pointing to the right. The tension in a piece of rope is the same everywhere along it.

Also, when you draw free body diagrams (FBD), you have to decide what the system is. This is particularly important when you have strings or ropes because the tension force is always away from the system. For this problem, I suggest that you draw a FBD for the knot at point B where the tensions in all three segments of rope come together. Then write your equations.

Two additional things to keep in mind: (a) Pulleys change the direction of the tension but not its magnitude; (b) the weights are not accelerating. What is the tension in the segments of rope attached to them?

 

[Steve4Physics]

@JohnnyLaws, have you met force triangles (for 3 forces in equilibrium)?

By using @kuruman's guidance and drawing the force triangle for the forces acting at point B, the problem can be solved very easily. (So easily that I can tell you the tension without doing any calculations! And the angle is almost as easy.)

By the way:
- use a small 'k' for kilo; capital 'K' means kelvin (a temperature unit);
- do not use 'string' or 'thread' to support 700kg - or there will will be a nasty accident. (Massless string in particular is a well known safety hazard.)

 

[Lnewqban]

... I believe I have explained everything in the "Relevant equations" section. What am I doing wrong? The book that I'm reading doesn't have any solutions.

Strings, ropes, cables and chains can only pull.
Therefore, there are three pulling forces acting on point B.
You know the magnitude and direction of two of them, the third one must induce a perfectly balance.