Finding the Area of a Sector using Trigonometric Functions

[chwala]

Homework Statement

See attached

Relevant Equations

Area of sector

My interest is on part (c) only.

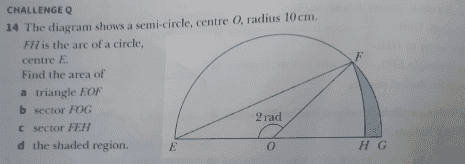
Wow, this was a nice one! boggled me a little bit anyways; my last steps to solution,
$A= \dfrac{1}{2} ×16.8319^2 × 0.5707=80.84cm^2$ bingo!
Any other approach apart from using sine?
Cheers guys

 

[BvU]

Any other approach apart from using sine?

Yes ! Using the cosine of angle FEH (which happens to be the sine of 1 radian, but that may well be a coincidence )

Your calculator needs new batteries: not 80.84 but 80.83 !

$\$