Finding the current in Field winding

[Physicslearner500039]

Homework Statement

In a shunt-wound dc motor with the field coils and rotor connected in parallel, the resistance Rf of the field coils is 106 Ohm and the resistance Rr of the rotor is 5.9 Ohm. When a potential difference of 120 V is applied to the brushes and the motor is running at full speed delivering mechanical power, the current supplied to it is 4.82 A. (a) What is the current in the field coils? (b) What is the current in the rotor? (c) What is the induced emf developed by the motor? (d) How much mechanical power is developed by this motor?

Relevant Equations

V = E + IR.

The problem seems to be easy but i don't get the correct answer.

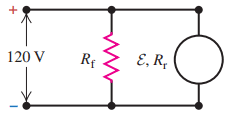
a. The current in the field coils. The net resistance of Rf = 106 and Rr = 5.9 is
$Reff = \frac {(106 * 5.9)} {(106.9 + 5.9)} = 5.54$
$\frac { 120 - E} {5.9} = 4.82 => E = 91.562$
$If = \frac { 120 - 91.562} {106} = 0.268 A$
The answer does not match. Please advise.

 

[cnh1995]

Your Reff is irrelevant. There are two voltage sources present in the circuit i.e. the supply voltage and the back emf.
As per your circuit diagram, what is the voltage across Rf? Then what is the current through Rf?

 

[Physicslearner500039]

Ok Understood, Thank You
$If = \frac {120} {106} = 1.13A$
$Ir = 4.82-1.13 = 3.68A$
$E = 120-3.68*5.9 = 98.2V$
$Pmech = 98.2*3.68 = 361 W$