Effect of different magnetic fields on a magnetic dipole

[zenterix]

Homework Statement

This question is about considering a magnetic dipole moment located at the origin of a coordinate system under effect of a magnetic field $\vec{B}$. For different definitions for $\vec{B}$, we need to find the net torque and the resultant force.

Relevant Equations

This is a problem from MIT OCW's online course 8.02. There is an automated solution system, but it only tells me what is wrong, not why. Thus, I spent an enormous amount of time today on this one problem without making too much progress.

Consider the following scenario.

We have a closed current loop (say a rectangular loop to make it easier) with magnetic dipole moment $\vec{\mu}$ shown below.

We have a magnetic field $\vec{B}$ which will be defined in different ways below.

I think it is easier to visualize as follows

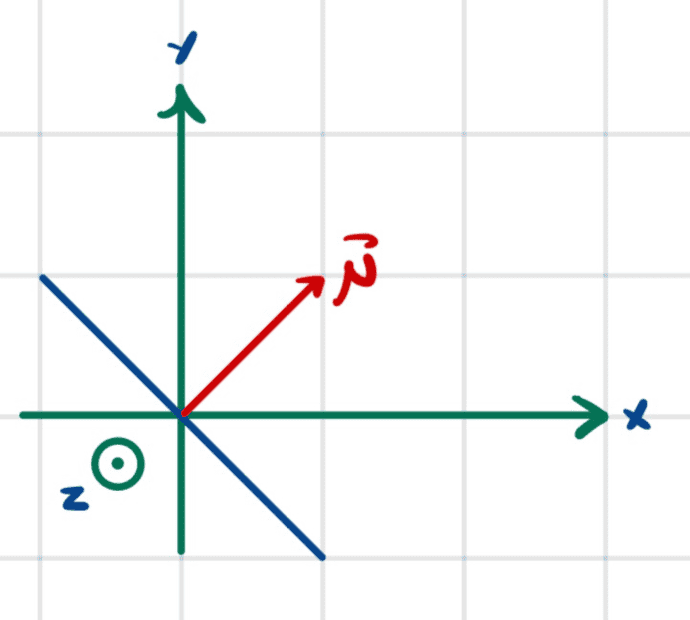
Where the blue line represents a side view of the current loop.

Let

$$\vec{\mu}=\mu_C(\hat{i}+\hat{j})$$

where $\mu_C$ is a positive constant.

Consider the following cases for the definition of magnetic field $\vec{B}$

a) $\vec{B}=B_0\hat{j}$

b) $\vec{B}=-B_0(\hat{i}+\hat{j}$

c) $\vec{B}=B_0\frac{x}{d}\hat{i}$

d) $\vec{B}=-B_0\frac{x}{d}\hat{j}$

e) $\vec{B}=B_0\frac{x^2}{d^2}\hat{j}$

f) $\vec{B}=B_0\left (\frac{x_0}{d}-\frac{x^2}{d^2}\right )\hat{j}$

where $x_0$ and $d$ are positive constants in units of meters and $x$ is the $x$ component of a point on the $xy$-plane.

The dipole is fixed so it cannot rotate or move.

We want to know the net torque and the resultant force.

Hence, essentially, we repeat the same analysis once for each of the items.

I thought this would be as simple as computing $\vec{\mu}\times \vec{B}$ in each case to obtain torque.

However, I think this only works in cases a) and b) since in the other cases the magnetic field depends on $x$.

Now, the calculations below are probably way overkill relative to what is required in this problem. However, I still think they should produce results that can answer this problem, albeit in a circuitous way. Yet, what I do below does not seem to produce the correct answers (at least according to the grading system).

One question I have is how to solve the problem in a simpler way using perhaps the given $\vec{\mu}$?

At some point I decided to do the calculations assuming that the current loop is rectangular.
The blue line in the picture above would then be one of the sides, and there would be two sides perpendicular to the screen (one with current going into the screen and the other with current coming out of the screen).

Here is another view

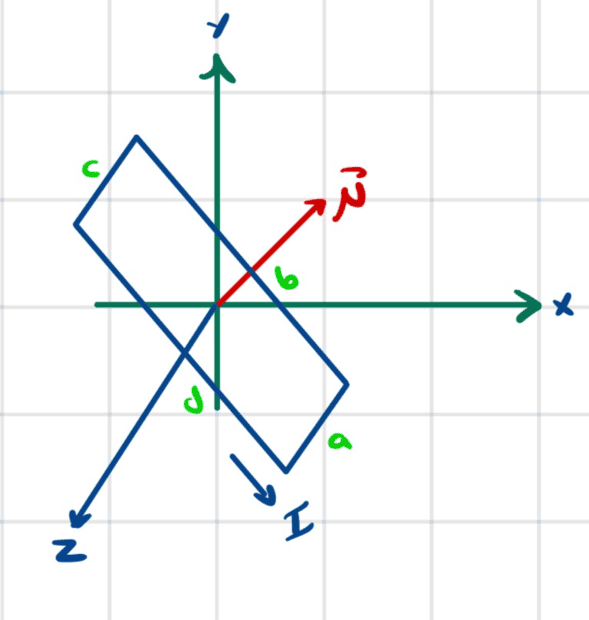
As far as I can tell, for this problem (in which $\vec{B}$ is always in the $xy$-plane) the only sides that contribute to net torque are (a) and (c) above. The forces on (b) and (d) cancel out in terms of torque and in terms of just their sum. Is this actually true? I did not try to do actual calculations, I simply contorted my right hand to figure out the right hand rule cross product for each piece of (b) and (d) in each case for $\vec{B}$.

For each case, I carried out the calculation

$$d\vec{F}_a(x,-x,z)=Id\vec{s}_a\times \vec{B}(x,-x,z)=Idz(-\hat{k}) \times\vec{B}(x,-x,z)$$

$$d\vec{F}_c(-x,x,z)=Id\vec{s}_c\times \vec{B}(-x,x,z)=Idz \hat{k} \times\vec{B}(-x,x,z)$$

$$\vec{F}_a= \int_a d\vec{F}_a=\int_{-l}^l \left (Idz(-\hat{k})\right )\times\vec{B}(x,-x,z)$$

$$\vec{F}_c=\int_c d\vec{F}_c=\int_{-l}^l (Idz\hat{k})\times\vec{B}(-x,x,z)$$

and then

$$\vec{\tau}=\int_a \vec{r}_a \times \vec{F}_a+\int_c \vec{r}_c\times\vec{F}_c$$

$$=\int_{-l}^l (x\hat{i}-x\hat{j}+z\hat{k})\times \vec{F}_a=\int_{-l}^l (-x\hat{i}+x\hat{j}+z\hat{k})\times\vec{F}_c$$

In other words, I compute the torque due to sides (a) and (c) be integrating the infinitesimal torques due to each piece of such sides.

Following are the results for each case.

Note that in each case, I am showing an array. The entries from top to bottom are $\vec{F}_a, \vec{F}_c, \vec{F}_a+\vec{F}_c$, and $\vec{\tau}$.

Note that $x>0$ and that $x$ is a constant.

The questions are

1) In which case (or cases) will the dipole experience a torque that tends to rotate it counterclockwise as viewed from $+z$?

2) In which case (or cases) will the dipole experience a torque that tends to rotate it clockwise as viewed from $+z$?

3) In which case (or cases) will the dipole experience no torque?

4) In which case (or cases) will the dipole experience a force that has a component in the $+x$ direction?

5) In which case (or cases) will the dipole experience a force that has a component in the $-x$ direction?

6) In which case (or cases) will the dipole experience a force that has a component in the $+y$ direction?

7) In which case (or cases) will the dipole experience a force that has a component in the $-y$ direction?

8) In which case (or cases) will the dipole experience no force?

My answer to these questions for the specific case of a rectangular loop are

1) (a) and (e). Also, (f) if $x^2<dx_0$.

2) Only (f) when $x^2>dx_0$.

3) (b), (c), (d)

4) None

5) (d)

6) None

7) (c)

8) (a), (b), (e), (f)

The solution system says 1), 3), 4), and 7) are incorrect.

 

[haruspex]

d) $\vec{B}=-B_0\frac{x}{c}\hat{j}$

c should be d?

As far as I can tell, for this problem (in which $\vec{B}$ is always in the $xy$-plane) the only sides that contribute to net torque are (a) and (c) above. The forces on (b) and (d) cancel out in terms of torque and in terms of just their sum.

Doesn't sound right to me.

 

[zenterix]

c should be d?

Doesn't sound right to me.

Yes, let me correct it.

 

[haruspex]

The forces on (b) and (d) cancel out in terms of torque and in terms of just their sum. Is this actually true?

In case c), $\vec B$ is along the x axis, so all four sides carry a current running the same way around it. Similarly case d).

 

[zenterix]

In case (c) here is what I can see

Note the purple arrows on the left picture shows $\vec{B}$. The magnitude increases as $x$ increases, and the direction depends on whether $x$ is positive or negative.

The forces on sides (b) and (d) cancel as far as I can tell.

 

[zenterix]

Here is case d)

Again the forces on (b) and (d) seem to cancel.

 

[haruspex]

In case (c) here is what I can see

View attachment 341591

Note the purple arrows on the left picture shows $\vec{B}$. The magnitude increases as $x$ increases, and the direction depends on whether $x$ is positive or negative.

The forces on sides (b) and (d) cancel as far as I can tell.

Sorry, I misunderstood your argument. In post #1 I thought you were saying it followed from $\vec B$ always being in the xy plane.
Your argument is, rather, that the field is antisymmetric about the yz plane in cases c and d, so creates opposing torques on sides a, c.

I don't understand your answers relating to case f. x has no particular value; it is a parameter to describe how the field varies in space. In your model, you would have to compare the dimensions of your loop with $x_0$, but in principle the cause of the magnetic dipole has no size.

 

[zenterix]

I don't understand your answers relating to case f. x has no particular value; it is a parameter to describe how the field varies in space. In your model, you would have to compare the dimensions of your loop with $x_0$, but in principle the cause of the magnetic dipole has no size.

The problem statement says that the dipole is held fixed.

We are simply analyzing the forces acting upon the dipole.

On segments (a) and (c), $x$ and $y$ are fixed and only $z$ varies. Thus, in all the integrals I showed, $x$ and $y$ are fixed (actually, given that we know that $\vec{\mu}$ is at $45^{\circ}$ I am using $x$ and $y=-x$ for (a) and then $-x$ and $y=x$ for (c)).

So for case $f$, $x$ is a constant. It simply depends on the size of the dipole being considered.

The value of $\vec{B}$ along (a) and (c) depends on the constant $x$ that is being used.

And you are right, I used this specific rectangular dipole to carry out calculations. For this dipole, the net torque seems to depend on what we choose $x$ to be.

I would also like to know how to solve the problem without resorting to this measure.

 

[zenterix]

Sorry, I misunderstood your argument. In post #1 I thought you were saying it followed from $\vec B$ always being in the xy plane.
Your argument is, rather, that the field is antisymmetric about the yz plane in cases c and d, so creates opposing torques on sides a, c.

Since $\vec{B}$ is only in the $xy$-plane and since current through (b) and (d) are flowing also in this plane then any magnetic force on any part of these segments is always pointing along the $\hat{k}$ direction.

I think you are right: by itself does not mean that there can not be torque. Note that any torque vector created by forces on (b) and (d) would have the same direction as $\vec{\mu}$.

What seems to make the torque on these specific segments (b) and (d) to be zero, however, is some kind of symmetry.

In cases c) and d), as you mention, there is an anti-symmetry about the $yz$-plane. But in case a) there is symmetry about that same plane. In case b) there is symmetry about the plane of the dipole itself.

In all these cases, for segments (b) and (d) the resulting forces cancel out and also produce no torque.

Here are cases a) and b)

 

[haruspex]

The problem statement says that the dipole is held fixed.

I did not suggest otherwise.

I am using $x$ and $y=-x$ for (a) and then $-x$ and $y=x$ for (c)).

So for case $f$, $x$ is a constant. It simply depends on the size of the dipole being considered.

I say again, the x in the expressions for $\vec B$ has no specific value, nor any relation to the dipole. It merely tells you how the field varies in space. You cannot reuse x as a parameter in your model and declare it to mean the same.

In fields c, d and e, the field is zero at the origin (and, indeed, everywhere in the yz plane). Taking the dipole as having no physical size, it would seem not to be subject to a field at all. But that's an idealisation, to which my approach is always to treat it as the limit of a sequence of realistic models.
Thus, you could take your loop as a square side s, figure out the net torque, then take the limit as s tends to zero.
For a side of the loop along which x varies, use an integral.

 

[zenterix]

You cannot reuse x as a parameter in your model and declare it to mean the same.

I am not sure what you mean.

Let's take case e), for example

$$\vec{B}(x,y,z)=B_0\frac{x^2}{d^2}\hat{j}$$

This field is constant along segments (a) and (c).

In the two integrals of $Id\vec{s}\times \vec{B}$ (one along (a) and one along (c), $x$ appears both in $d\vec{s}$ and $\vec{B}$ as a constant in the integral.

We compute the two integrals given an $x$.

It is a parameter, yes, based on the dimension of the rectangular loop being used.

The $x$ in $\vec{B}(x,y,z)$ is just a variable We actually have $\vec{B}(\vec{r}(x,y,z))=\vec{B}(x\hat{i}+y\hat{j}+z\hat{k})$. We could use different names for $x,y,z$.

The integrals I computed are only in $z$ however, so when I write $\vec{B}(x,-x,z)$, $x$ is no longer a variable but a constant.

Here is my little diagram for case f) btw

 

[zenterix]

In fields c, d and e, the field is zero at the origin (and, indeed, everywhere in the yz plane). Taking the dipole as having no physical size, it would seem not to be subject to a field at all. But that's an idealisation, to which my approach is always to treat it as the limit of a sequence of realistic models.
Thus, you could take your loop as a square side s, figure out the net torque, then take the limit as s tends to zero.
For a side of the loop along which x varies, use an integral.

Why are we speaking of the limit of zero?

Doesn't the fact that we have $\vec{\mu}=\mu_C(\hat{i}+\hat{j})$ that $IA=\mu_C>0$ and so $A>0$?

That is, the dipole loop has area.

 

[haruspex]

I am not sure what you mean.

In your answers you referred to x as though it had some specific value, "if $x^2<dx_0$”.
That cannot be a valid answer. You can specify the dimensions of your model in terms of some variables you define, such as X and Y, but better not to cause confusion by calling them x. You can also use x as a variable referring to the x coordinates of a particular point in your loop, since that conforms to the given usage. But your answer would then mention X and/or Y instead, so still does not constitute a valid answer since those are not given.

Why are we speaking of the limit of zero?

Doesn't the fact that we have $\vec{\mu}=\mu_C(\hat{i}+\hat{j})$ that $IA=\mu_C>0$ and so $A>0$?

That is, the dipole loop has area.

I see nothing in the problem statement about I or A. In almost any real situation there will be a nonzero A and I (an exception being an electron), but when you are just given the dipole moment you cannot assume any substantial size. Electric dipoles are generally taken to be arbitrarily small, so I suspect the same applies to magnetic ones.
Whatever, if the question makes sense it should not depend on A. You can take the limit as A tends to zero while $\vec \mu$ remains constant (and, yes, I tending to infinity).

 

[zenterix]

@haruspex Let's just consider case f).

I just want to make sure of one thing. $x_0>0$ is a parameter in the definition of $\vec{B}$ and $x$ is an independent variable in this definition.

Therefore, is it not true that for a rectangular loop (with sides (a) and (c) having $x$-coordinate $x_1$ and $-x_1$, for $x_1>0$) the net torque depends on the relationship between $x_0$ and $x_1$?

Do you agree with this statement?

In particular, if $x_1>x_0$ then torque is in $-\hat{k}$ direction, and if $x_1<x_0$ then torque is in the $|hat{k}$ direction.

 

[haruspex]

@haruspex Let's just consider case f).

I just want to make sure of one thing. $x_0>0$ is a parameter in the definition of $\vec{B}$ and $x$ is an independent variable in this definition.

Therefore, is it not true that for a rectangular loop (with sides (a) and (c) having $x$-coordinate $x_1$ and $-x_1$, for $x_1>0$) the net torque depends on the relationship between $x_0$ and $x_1$?

Do you agree with this statement?

In particular, if $x_1>x_0$ then torque is in $-\hat{k}$ direction, and if $x_1<x_0$ then torque is in the $|hat{k}$ direction.

I agree with all that in regard to a and c, except that it also depends on the parameter d as you noted in post #1. I.e. $x_1^2<>x_0d$.
For b and d it is more complicated since the torque varies along them. In particular, for $x_1^2>x_0d$ the torque is one way at their ends and the other way at their centres. Thus the boundary value for $x_1^2$, where the net torque switches sign, will be a bit greater than $x_0d$.

However, as I wrote, I think you should be considering the limit $x_1\rightarrow 0$.

 

[haruspex]

I went through my limit method. It says, as I rather suspected, that c, d and e all give zero torque because the field at the origin is zero.
If that is wrong then I have no idea what the question means. But it is consistent with the marking you got on 1, 2 and 3.

I'll look at forces next.

 

[haruspex]

For forces, I took https://pubs.aip.org/aapt/ajp/article-abstract/56/8/688/572081/The-force-on-a-magnetic-dipole as authority.
I found the force to be zero except for c and d. For c, the two models of dipole described at the link give the same answer; for d they have the same magnitude but different directions ($\hat i$ versus $\hat j$).

 

[kuruman]

What has concerned me about this is that the statement of the problem mentions "a magnetic dipole moment located at the origin of a coordinate system" which OP has interpreted to be a rectangular loop with finite-sized sides and forces acting on each side. I think the intent of the problem is to have a point dipole moment at the origin. Torques and forces are to be calculated using, respectively, $\vec {\tau}=\vec m\times \vec B$ and $\vec F=\vec {\nabla}(\vec m\cdot \vec{B}).$

To @zenterix: Can you provide the link to this problem?

 

[haruspex]

I think the intent of the problem is to have a point dipole moment at the origin.

Yes, that is the view I have been pushing.

Torques and forces are to be calculated using, respectively, $\vec {\tau}=\vec m\times \vec B$ and ##\vec F=\vec {\nabla}(\vec m\cdot \vec{B}).#

What about the model choice for the dipole mentioned at the link I posted in #17?

 

[kuruman]

Yes, that is the view I have been pushing.

What about the model choice for the dipole mentioned at the link I posted in #17?

I looked at the Abstract of the article. I have not read the body of the article so I cannot see the difference between $\mathbf{F}=\mathbf{\nabla}(\mathbf{m}\cdot\mathbf{B})$ and $\mathbf{F}=(\mathbf{m}\cdot\mathbf{\nabla})\mathbf{B}.$

It seems to me that if one uses the product rule identity and the fact that the dipole moment has no spatial dependence, $$\mathbf{F}=\mathbf{\nabla}(\mathbf{m}\cdot\mathbf{B})=(\mathbf{m}\cdot\mathbf{\nabla})\mathbf{B}+\mathbf{m}\times\left(\mathbf{\nabla}\times\mathbf{B}\right).$$ So far so good. Perhaps here is where the model enters the picture. If I think of $\mathbf{m}$ as the magnetic dipole of, say, an electron, then there is no current $\mathbf{J}$ anywhere and, by Maxwell's equation, $\mathbf{\nabla}\times\mathbf{B}=0.$ Hence, $$\mathbf{F}=\mathbf{\nabla}(\mathbf{m}\cdot\mathbf{B})=(\mathbf{m}\cdot\mathbf{\nabla})\mathbf{B}.$$ Maybe I will read the article tomorrow. It's late where I am and I have to sign off before I say anything stupid.

 

[haruspex]

$\vec m=\mu(\hat i+\hat j)$
In case d), $\vec B=-x\hat j$
$\vec m\cdot \vec B= -\mu x$
$\nabla(\vec m\cdot \vec B)= -\mu \hat i$
$\vec m\cdot\nabla=\mu(\frac{\partial}{\partial x}+\frac{\partial}{\partial y})$
$(\vec m\cdot\nabla)\vec B=-\mu\hat j$
Do I have something wrong?

 

[zenterix]

Can you provide the link to this problem?

The problem is from a course on MIT's Open Learning Library (8.02, Electromagnetism). I think you have to be logged in to access it. Here is a screenshot

 

[zenterix]

Torques and forces are to be calculated using, respectively, τ→=m→×B→ and F→=∇→(m→⋅B→).

I also think that this is the intent of the problem.

 

[kuruman]

$\vec m=\mu(\hat i+\hat j)$
In case d), $\vec B=-x\hat j$
$\vec m\cdot \vec B= -\mu x$
$\nabla(\vec m\cdot \vec B)= -\mu \hat i$
$\vec m\cdot\nabla=\mu(\frac{\partial}{\partial x}+\frac{\partial}{\partial y})$
$(\vec m\cdot\nabla)\vec B=-\mu\hat j$
Do I have something wrong?

Not really wrong. Just incomplete. I read the article and I show below a screenshot of the relevant excerpt.

With $~\mathbf{B}=-\dfrac{x}{d}\mathbf{\hat j}~$ and $~\mathbf{m}=\mu(\mathbf{\hat i}+\mathbf{\hat j})$,$$\mathbf{m}\cdot\mathbf{B}=-\dfrac{\mu~x}{d}\implies \mathbf{\nabla}(\mathbf{m}\cdot\mathbf{B})=-\dfrac{\mu}{d}\mathbf{\hat i}$$ as you found (for $d=1$).

It is also true that $~(\mathbf{m}\cdot\mathbf{\nabla})\mathbf{B}=-\dfrac{\mu}{d}\mathbf{\hat j}~$ as you found.

However, to complete the picture, there is an additional term to be calculated. $$\mathbf{\nabla}\times(\mathbf{\nabla}\times\mathbf{B})=\mu(\mathbf{\hat i}+\mathbf{\hat j})\times(-\frac{1}{d}\mathbf{\hat k})=\frac{\mu}{d}\mathbf{\hat j}-\frac{\mu}{d}\mathbf{\hat i}.$$Therefore $$\mathbf{\nabla}(\mathbf{m}\cdot\mathbf{B})=-\dfrac{\mu}{d}\mathbf{\hat i}=(\mathbf{m}\cdot\mathbf{\nabla})\mathbf{B}+\mathbf{\nabla}\times(\mathbf{\nabla}\times\mathbf{B})$$ which verifies the identity.

This confirms that my assertion in post #20 that $\mathbf{J}=0$ was unwarranted. Although the problem does not mention currents, I should have seen that the curl of the magnetic field is non-zero. The moral of the story here is "use $~\mathbf{F}=\mathbf{\nabla}(\mathbf{m}\cdot\mathbf{B})~$ and you can't go wrong."

 

[kuruman]

Thank you for posting the screenshot of the problem.

I also think that this is the intent of the problem.

Then forget the rectangular current loop. Use the solution for part (d) above as a template.

 

[zenterix]

I'm going to read the article and come back here.