Finding the currents in this circuit (2 voltage sources and 3 resistors)

[Nat1234123]

Homework Statement

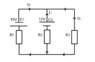
Which current ratings do I1, I2 and I3 have if the resistances hold R1 = 0.1 ohm, R2 = 0.02 Ohm and R3 = 0.2 Ohm?

Relevant Equations

U = IR
1/R = 1/R_1 + 1/R_2 + ....
I1 = I2 + I3

In my attempt, I tried
1) I1 = I2 + I3
Then set up these two equations based on Kirchhoff's second rule:
2) U1 = R1 (I2) + R3 (I3) and
3) U1 + U2 = R1 (I1) + R2 (I3).
From what we have
10 = 0.1* I_2 + 0.2 * I_3
22 = 0.1* I_2 + 0.02*I_3

I_3 = 50 - 0.5 I_2

That means
I_2 = 233.3 A
I_3 = -66.7A
I1 = 166.6A
My answer is completely off.

 

[phinds]

In my attempt, I tried
1) I1 = I2 + I3

That does not comport with your drawing.

 

[Nat1234123]

That does not comport with your drawing.

If I fix that part, will the rest be right then?

 

[phinds]

If I fix that part, will the rest be right then?

No. Start there and rework the problem.

 

[erpelkon]

Substitute I3=z, I2=y and I1=x.

System of equations:
z = y + x
12−0.2z−0.02x=0
−10+0.2z+0.1y=0

From second and third equation solve:
x=−10z+600
y=100−2z

Add these to the first:
z=(100−2z)+(−10z+600)
z=700/13
z~53,85

Thus I3~53,85 , I2~-7,7 and I1~61,5

Hope this helps!

 

[SammyS]

Substitute I3=z, I2=y and I1=x.

System of equations:
z = y + x
12−0.2z−0.02x=0
−10+0.2z+0.1y=0
. . .

Hope this helps!

Your second loop equation (the last equation I quoted above) is incorrect. Which direction around the loop did you use?

 

[erpelkon]

Your second loop equation (the last equation I quoted above) is incorrect. Which direction around the loop did you use?

How come? Clockwise, i.e. U2 is positive direction and U1 is negative direction.

 

[SammyS]

How come? Clockwise, i.e. U2 is positive direction and U1 is negative direction.

Previously I quoted the following from your Post #5.

Substitute I3=z, I2=y and I1=x.

System of equations:
z = y + x
12−0.2z−0.02x=0
−10+0.2z+0.1y=0

The loop equation I referred to is:
$\displaystyle \quad −10+0.2z+0.1y=0 \$.

You are correct in that going clockwise around the outer loop the voltage contribution from $U_1$ is $-\,10$ volts. However, the clockwise direction around this loop is also consistent with the given choice of current direction for both $I_2$ and $I_3$, so both give voltage drops (negative) across their respective resistors. In other words that loop equation should be:

$\displaystyle \quad -U_1-I_3 R_3 - I_2 R_1 = 0$ .Your other equations are correct.

 

[erpelkon]

View attachment 337612
Previously I quoted the following from your Post #5.

The loop equation I referred to is:
$\displaystyle \quad −10+0.2z+0.1y=0 \$.

You are correct in that going clockwise around the outer loop the voltage contribution from $U_1$ is $-\,10$ volts. However, the clockwise direction around this loop is also consistent with the given choice of current direction for both $I_2$ and $I_3$, so both give voltage drops (negative) across their respective resistors. In other words that loop equation should be:

$\displaystyle \quad -U_1-I_3 R_3 - I_2 R_1 = 0$ .Your other equations are correct.

So basically higher voltage U2 is "charging" lower voltage U1 since given the orientation of U1 the current is reversed! Agreed!

 

[SammyS]

So basically higher voltage U2 is "charging" lower voltage U1 since given the orientation of U1 the current is reversed! Agreed!

I wouldn't put it that way, because you will find out that $I_2$ (which you relabeled as y) is negative, so the current flows through $U_1$ from the negative terminal to the positive terminal, opposite the direction chosen for $I_2$ in your drawing.

 

[erpelkon]

I wouldn't put it that way, because you will find out that $I_2$ (which you relabeled as y) is negative, so the current flows through $U_1$ from the negative terminal to the positive terminal, opposite the direction chosen for $I_2$ in your drawing.

But after calculus one will find out I1 to be the largest and not I3, thus U1 has to be a load and not a source?