MHB Finding the distance between a point and a line

[MarkFL]

In analytic or coordinate geometry, we are often asked to work problems that involve using the perpendicular (shortest) distance between a point and a line in the plane. Here are two methods to find this distance:

Method 1:

In the xy plane, we have a point $\displaystyle P_0\left(x_0,y_0 \right)$ separated from a line $\displaystyle y=mx+b$ by some distance $\displaystyle d>0$.

Extend a line segment from the point to the line such that the segment intersects perpendicularly with the line y. Label this segment d.

Now extend a vertical line segment from the point to the line and we find its length is $\displaystyle a=\left|mx_0+b-y_0 \right|$ (using $\displaystyle y\left(x_0 \right)-y_0$).

Next, extend a horizontal line segment from the point to the line and we find its length is $\displaystyle c=\left|x_0-\frac{y_0-b}{m} \right|$ (using $\displaystyle x_0-x\left(y_0 \right)$) thus:

$\displaystyle c=\left|\frac{mx_0+b-y_0}{m} \right|=\frac{a}{|m|}$

Please refer to the diagram:

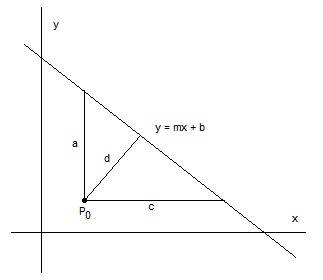
By similarity, we have:

$\displaystyle \frac{d}{c}=\frac{\sqrt{a^2-d^2}}{a}$

$\displaystyle \frac{d}{\sqrt{a^2-d^2}}=\frac{c}{a}=\left|\frac{1}{m} \right|$

$\displaystyle \frac{d^2}{a^2-d^2}=\frac{1}{m^2}\:\therefore\:d^2=\frac{a^2}{m^2+1}\:\therefore\:d=\frac{a}{\sqrt{m^2+1}}$

Thus, we have:

$\displaystyle d=\frac{\left|mx_0+b-y_0 \right|}{\sqrt{m^2+1}}$

Method 2:

First, we find that the line perpendicular to $\displaystyle y=mx+b$ and passing through $\displaystyle P_0$ is:

$\displaystyle y=-\frac{1}{m}\left(x-x_0 \right)+y_0$

Solving the resulting linear system we find the common point to both lines is:

$\displaystyle \left(\frac{x_0+m\left(y_0-b \right)}{m^2+1},\frac{m\left(x_0+my_0 \right)+b}{m^2+1} \right)$

Now, using the distance formula for $\displaystyle P_0$ to the above point, we find:

$\displaystyle d=\sqrt{\left(x_0-\frac{x_0+m\left(y_0-b \right)}{m^2+1} \right)^2+\left(y_0-\frac{m\left(x_0+my_0 \right)+b}{m^2+1} \right)^2}$

The reader should verify that this reduces to:

$\displaystyle d=\frac{\left|mx_0+b-y_0 \right|}{\sqrt{m^2+1}}$

Comments and questions should be posted here:

http://mathhelpboards.com/commentary-threads-53/commentary-finding-distance-between-point-line-5966.html

 

[MarkFL]

This topic is for comments/questions pertaining to this tutorial:

http://mathhelpboards.com/math-notes-49/finding-distance-between-point-line-2952.html

 

[caffeinemachine]

This topic is for comments/questions pertaining to this tutorial:

http://mathhelpboards.com/math-notes-49/finding-distance-between-point-line-2952.html

There is another nice way to do it.

Let $C$ be the circle $(x-x_0)^2+(y-y_0^2)=r^2$ centered at $P$ and having radius $r$. The line $y=mx+b$ can have two points in common or one point in common or no points on common with $C$. Assume $m\neq 0$ because if it is then the answer is easily found. The perpendicular distance from $P$ to $y=mx+b$ is equal to the radius $r$ corresponding to which there is exactly one point in common between $y=mx+b$ and $C$. For this we substitute $x=(y-b)/m$ in $C$ and find a quadratic in $y$. For having just one root of this we just need to set the discriminant to zero and find the desired result.

 

[Evgeny.Makarov]

I suggest the following proof that deals with the general (or standard) form of the line equation rather than the slope–intercept form.

Suppose in a Cartesian coordinate system a line $l$ is given by the equation $L(x,y)=0$ where $L(x)=Ax+By+C$. Also, let $\vec{n}=(A,B)$.

Theorem. The distance $d(P_0,l)$ from any point $P_0(x_0,y_0)$ to $l$ is $L(x_0,y_0)/|\vec{n}|$.

Proof. Let $P_1(x_1,y_1)$ be any point on $l$ (thus, $L(x_1,y_1)=0$) and let $\varphi$ be the (smaller) angle between $\overrightarrow{P_1P_0}$ and $\vec{n}$. Since $\vec{n}$ is perpendicular to $l$ (Lemma 2 below), we have
\begin{align*}
d(P_0,l)&= |\overrightarrow{P_1P_0}|\cdot|\cos\varphi|\\
&=\frac{|\overrightarrow{P_1P_0}\cdot\vec{n}|} {|\vec{n}|}\\
&= \frac{|A(x_0-x_1)+B(y_0-y_1|)}{|\vec{n}|}\\
&=\frac{|L(x_0,y_0)-L(x_1,y_1)|}{|\vec{n}|}\\
&=\frac{|L(x_0,y_0)|}{|\vec{n}|}
\end{align*}

Since $|\vec{n}|=\sqrt{A^2+B^2}$, $d(P_0,l)$ can be expanded to
\[
\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}
\]

Lemma 1. Vector $(-B,A)$ is parallel to $l$. This holds in any affine coordinate system, not necessarily a Cartesian one.

Proof. Let $P_0(x_0,y_0)$, $P_1(x_1,y_1)$ be two different points on $l$. Then $\overrightarrow{P_0P_1}=(x_1-x_0,y_1-y_0)$ is parallel to $l$. Also,
\[
L(x_1,y_1)-L(x_1,y_1)=A(x_1-x_0)+B(y_1-y_0)=0
\]
or
\[
A(x_1-x_0)=-B(y_1-y_0)\tag{*}
\]
If $A\ne0$ and $B\ne0$, then (*) is equivalent to
\[
\frac{x_1-x_0}{-B}=\frac{y_1-y_0}{A}
\]
But even if $A=0$ or $B=0$ (but not $A=B=0$), (*) expresses the fact that $(x_1-x_0,y_1-y_0)$ is proportional to, and thus parallel to, $(-B,A)$.

Lemma 2. If the coordinate system is Cartesian, then $n$ is perpendicular to $l$.

Proof. By Lemma 1, vector $\vec{p}=(-B,A)$ is parallel to $l$, and $\vec{n}\cdot\vec{p}=-AB+BA=0$, so $n$ is perpendicular to $p$ and to $l$.