- #1
NODARman
- 57
- 13
- TL;DR Summary
- .
Hi, I'm trying to solve the problem from here: https://www.physics.uoguelph.ca/chapter-1-newtonian-mechanics
Exercise 1.1: Determine how the coordinates $$x$$ and $$y$$, as well as the basis vectors $$\hat{x}$$ and $$\hat{y}$$, change under a rotation around the $$z$$ axis by an angle $$α$$. Then show mathematically that the $$r$$ vector is invariant under the transformation.
I wrote this and want to know if it's correct and how to continue:
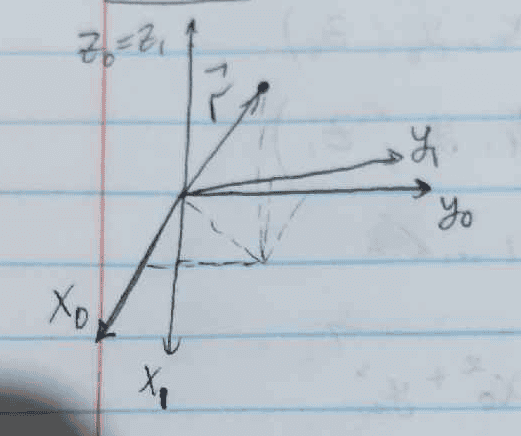
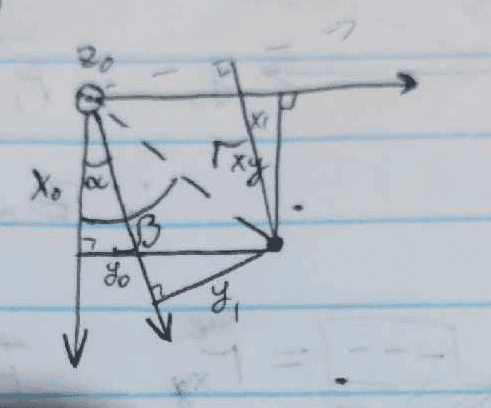
$$r_{x y}=\sqrt{x_0^2+y_0^2}$$
$$
\sin (\beta-\alpha)=\frac{y_1}{r_{xy}}=\sin \beta \cos \alpha-\cos \beta \sin \alpha
$$
$$
\sin (\beta-\alpha)=\frac{y_1}{\sqrt{r}_{xy}}=\sin \beta \cos \alpha-\cos \beta \sin \alpha
$$
$$
\cos \beta=\frac{x_0}{r_{x y}}
$$
$$
\sin \beta=\frac{y_0}{r_{x y}}
$$
$$
\begin{array}{l}
x_1=r_{x y} \cos \alpha \cos \beta+r_{x y} \sin \alpha \sin \beta \\
y_1=r_{x y} \sin \beta \cos \alpha-r_{x y} \cos \beta \sin \alpha
\end{array}
$$
$$
\begin{array}{l}
x_1=x_0 \cos \alpha+y_0 \sin \alpha \\
y_1=y_0 \cos \alpha-x_0 \sin \alpha
\end{array}
$$
$$
z_0=z_1
$$
$$
\vec{r}_0=\left(x_0 ; y_0 ; z_0\right)
$$
$$
\vec{r}_1=(x_1 ; y_1 ; z_1) = [(x_0 \cos \alpha+y_0 \sin \alpha ) ; (y_0 \cos \alpha-x_0 \sin \alpha) ; z_0]
$$
Exercise 1.1: Determine how the coordinates $$x$$ and $$y$$, as well as the basis vectors $$\hat{x}$$ and $$\hat{y}$$, change under a rotation around the $$z$$ axis by an angle $$α$$. Then show mathematically that the $$r$$ vector is invariant under the transformation.
I wrote this and want to know if it's correct and how to continue:
$$r_{x y}=\sqrt{x_0^2+y_0^2}$$
$$
\sin (\beta-\alpha)=\frac{y_1}{r_{xy}}=\sin \beta \cos \alpha-\cos \beta \sin \alpha
$$
$$
\sin (\beta-\alpha)=\frac{y_1}{\sqrt{r}_{xy}}=\sin \beta \cos \alpha-\cos \beta \sin \alpha
$$
$$
\cos \beta=\frac{x_0}{r_{x y}}
$$
$$
\sin \beta=\frac{y_0}{r_{x y}}
$$
$$
\begin{array}{l}
x_1=r_{x y} \cos \alpha \cos \beta+r_{x y} \sin \alpha \sin \beta \\
y_1=r_{x y} \sin \beta \cos \alpha-r_{x y} \cos \beta \sin \alpha
\end{array}
$$
$$
\begin{array}{l}
x_1=x_0 \cos \alpha+y_0 \sin \alpha \\
y_1=y_0 \cos \alpha-x_0 \sin \alpha
\end{array}
$$
$$
z_0=z_1
$$
$$
\vec{r}_0=\left(x_0 ; y_0 ; z_0\right)
$$
$$
\vec{r}_1=(x_1 ; y_1 ; z_1) = [(x_0 \cos \alpha+y_0 \sin \alpha ) ; (y_0 \cos \alpha-x_0 \sin \alpha) ; z_0]
$$