Finding the frequency of noisy data for a pulse sensor

[wolfpax50]

I have a simple home built pulse sensor that uses light from an LED to measure the opacity of my skin. As my heart beats the opacity of my skin goes up an down in a saw tooth like pattern. The frequency of this wave is my heat beat. The frequency is easy enough to find manually (by counting the peaks) but I want a mathematical solution so I can have a computer find my heart rate for me.

Put in mathematical terms, I need to find the frequency of a noisy wave function.

Also, because the sensor is affected by other light sources other than the LED the data may not be normalized. For example, the little peaks and troughs might represent my heartbeat but a big peak or trough might represent me turning a light on in the room, or shifting the sensor.

Here is an example of what my data looks like (from another person's similar sensor):

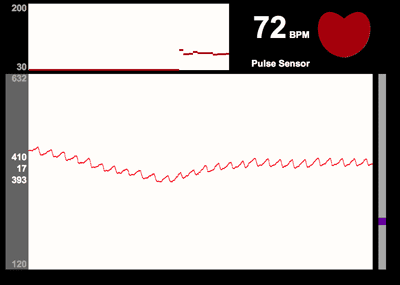
How could I go about doing this?

 

[Vargo]

Hi Wolfpax.

My first suggestion would be to ask this in the electrical engineering forum because there are likely experts there who could spell it all out for you.

But, since you asked here I will give you what answer I can. I believe you'll want to use a discrete Fourier transform here. Your sensor is collecting data x(t). You'll want to sample that data at regular time intervals to get a sequence of values x_0, x_1, \dots, x_{N-1}
The frequency of sampling should be at least double whatever your maximum expected frequency of heart rate. Ok, now you take that data and do a Discrete Fourier Transform on it. That gives you a new sequence of complex numbers X_i. The formula is
$$ X_k = \sum_{k=0}^{N-1} x_k e^{-i2\pi kn/N}.$$
That formula along with more info is at http://en.wikipedia.org/wiki/Discrete_Fourier_transform
It might be better if you use an algorithm for the Fast Fourier Transform instead of this formula because that is very efficient. I don't know about such things though.

The coefficient X_k tells you the "strength" of the frequency kn / N. Pick out the largest coefficient (measured by the modulus of the number because it is a complex number), and the corresponding frequency is the one you are looking for.

This will tell you the heart rate over the time interval you sampled over. You can't get an "instantaneous" frequency, but given the regularity of your data it would probably be fine to have your sample just go over the last 5 seconds or so and measure the frequency in that interval. That way you could at all times keep track of your heart rate from the last 5 seconds.

That's a starting point. If you take this to the electrical engineers, they could hopefully give you more specific information and correct any mistakes in what I have written.

 

[wolfpax50]

Thanks, that is exactly what I was looking for. I posted here because I figured it had more to do with math than electricity. I appreciate the help.

 

[AlephZero]

You could do this by Fourier analysis, but it would probably be easier to write a program to just "count the peaks" the same way as you do it by hand.

Pick a sampling rate so you get a reasonable number of samples per heartbeat, but not so many that you get a lot of high frequency noise. Maybe 20 samples per beat or about 25 samples per second would be a good start. Then define a "peak" as when the middle sample of a group of say 5 or 7 samples is the biggest values, so the counting doesn't get thrown if a noisy signal gives you two "peaks" close together. (That is just making software "know" that your heart rate can't possibly be a ridiculously high number like 1000 beats /minute). Then average over a few beats (or a few seconds of data). Or you could make the program to show the range of values, so you can see how "steady" the beat is as well as its speed.

With this sort of data analysis problem, there are times to use advanced math, but there are also times when the best way is to do something simple and "bulletproof".

 

[wolfpax50]

That's what I had been doing before. It works fine, but every so often it'll miss or double count a beat. And a single error can really throw off the average. I thought a more analytical solution would be more resistant to such errors because it would be looking at the whole wave and not just the peaks.

 

[AlephZero]

That's what I had been doing before. It works fine, but every so often it'll miss or double count a beat. And a single error can really throw off the average. I thought a more analytical solution would be more resistant to such errors because it would be looking at the whole wave and not just the peaks.

There are numerical methods that would probably be "better", but a Fourier analysis like Vargo described might not do what you want. If you want to measure to say 1 beat per minute by looking for the peaks in an FFT as Vargo suggested, you will have to a sample of at least 1 minute of data and you will be assuming the heart rate is constant for that time. This is independent of the sampling rate. If you take more samples per second, the FFT will gives you a wider range of frequences (which is irrelevant for what you want), but it won't give you any more accuracy.

If you are looking at recovery from exercise, etc, assuming the heart rate is constant for as long as a minute doesn't seem very useful.

There are methods to estimate the dominant frequences from a shorter data samples without beiing "locked in" to the sampling rate, for example methods based on autocorrelation, but this quickly gets into some advanced (graduate school level) math.