PainterGuy
- 938
- 73
- Homework Statement
- I'm trying to find the general solution of nonhomogeneous linear system.
- Relevant Equations
- I've presented my work below.
Hi,
I was trying to do the following problem.
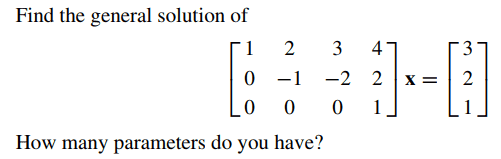
My attempt.
Finding the reduced row echelon form for the system above.
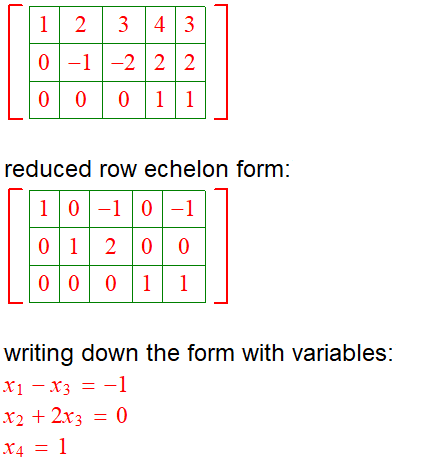 I do not see any way to proceed any further. The following is the solution presented in solution manual. How do I proceed to get the following answer?
I do not see any way to proceed any further. The following is the solution presented in solution manual. How do I proceed to get the following answer?
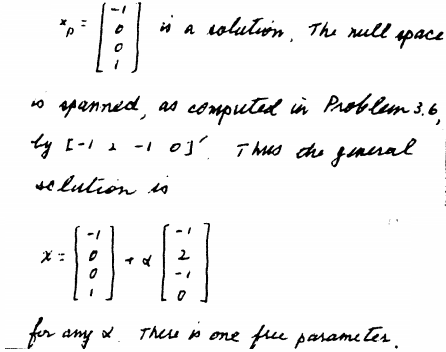
I was trying to do the following problem.
My attempt.
Finding the reduced row echelon form for the system above.