- #1
jjr
- 51
- 1
Homework Statement
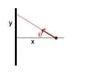
A homogeneous rod with even thickness has mass M and length L.
a) Find the gravitational field g(x) at a distance x from the rod on an axis normal to the midpoint of the rod.
b) Find the gravitational field g(y) at a distance y from the rod's midpoint on an axis through the rod in the direction of its length.
Homework Equations
Gravitational potential V(r) = -GM/r (1)
Gravitational field g(r) = -∇V(r) (2)
Where G is the gravitational constant, M is the mass of the relevant object and r is the distance from the object.
The Attempt at a Solution
a) My plan was to first work out the gravitational potential through integrating the contributions from infinitesimal lengths of the rod (from -L/2 to L/2) and then use equation (2) to find the field. The mass per length of the road is μ = M/L, so an infinitesimal piece of the rod dm = μ dl, where dl is an infinitesimal length. I got dV(r) = -[itex]\frac{G dm}{r}[/itex] = -[itex]\frac{G μ dl}{r}[/itex]. The r is (pythagoras) √(x2 + l2), where l is the distance from the midtpoint of the rod. The problem arises when I try to integrate this function dV(r) = -[itex]\frac{G μ dl}{√(x^2 + l^2)}[/itex] from -L/2 to L/2. Here's when I get in trouble. This integral is a bit hairier than expected, and I find it hard to get a reasonable answer. Could someone point me in the right direction here?
I'll post my attempts at the solution for b) if I can't figure it out after getting help with a).
Thanks,
J