SUMMARY
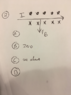
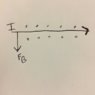
This discussion focuses on calculating the current (I) flowing through a wire using the formula F = ILA, where F is the force, L is the length of the wire, and A is the area of the magnetic field. The participants clarify that the magnetic field (B) generated by the wire does not support the wire's weight and emphasize the importance of understanding the forces in equilibrium. The correct approach to find the current involves manipulating the equation I = F / (LB), where B is the magnetic field strength, and L is the length of the wire segment.
PREREQUISITES
- Understanding of electromagnetism principles
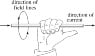
- Familiarity with the right-hand rule for magnetic fields
- Knowledge of force equations in physics
- Basic concepts of magnetic fields around current-carrying wires
NEXT STEPS
- Study the derivation and application of the formula F = ILA
- Learn about the equilibrium of forces in electromagnetic systems
- Explore the concept of magnetic fields generated by current-carrying conductors
- Investigate the right-hand rule and its applications in electromagnetism
USEFUL FOR
Students studying physics, particularly those focusing on electromagnetism, as well as educators and tutors seeking to clarify concepts related to current and magnetic fields.