bergausstein
- 191
- 0
please help me solve the problem graphically,
what I know is that eventually I 'm going to be using law of sine and law of cosine for this problem. my problem is how to determine the necessary angle to be used in that method.
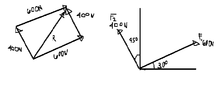
this is how far I can get to, I use parallelogram rule and I'm stuck. please help.
find R and $\theta_R$
what I know is that eventually I 'm going to be using law of sine and law of cosine for this problem. my problem is how to determine the necessary angle to be used in that method.
this is how far I can get to, I use parallelogram rule and I'm stuck. please help.
find R and $\theta_R$
Attachments
Last edited: