CivilSigma
- 227
- 58
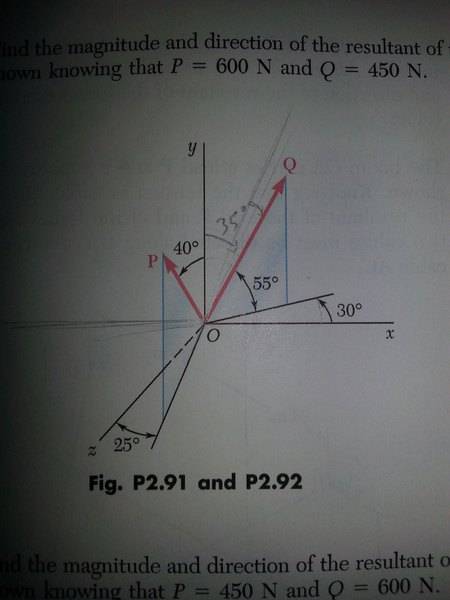
Hi, For the following image, we have to calculate the resultant of those two forces. I have broken them down to their components. Did I do this correctly because when I actually solve for the force I am not getting the correct answer of 940N in the back of my book.
Also, I tried calculating the direction of force P in the x plane , Q in the z plane and when I used the cosine formula I got
cos^2 theta = -0.4 ( a negative number) does that imply that our vector does not exist in the x plane and therefore is 0 for P? and 0 for Q in the z plane?
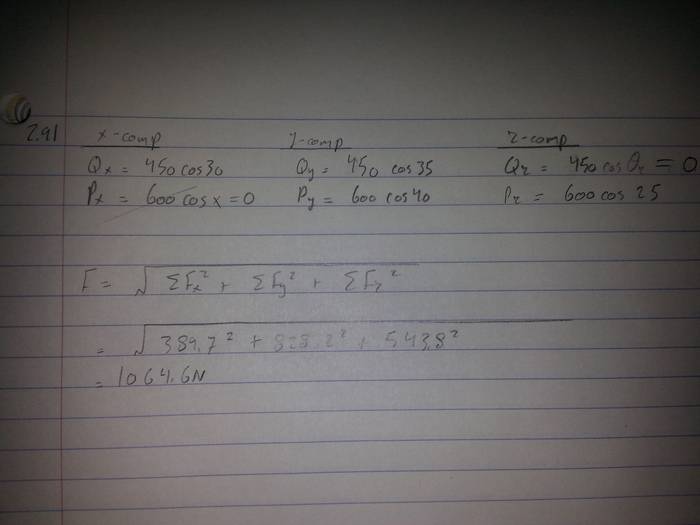
Also, I tried calculating the direction of force P in the x plane , Q in the z plane and when I used the cosine formula I got
cos^2 theta = -0.4 ( a negative number) does that imply that our vector does not exist in the x plane and therefore is 0 for P? and 0 for Q in the z plane?