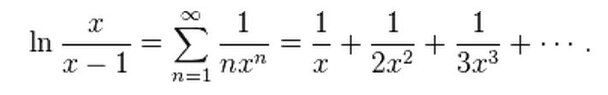Finding the Sum of a Tricky Series

[Pull and Twist]

Find the sum of $$\sum_{n=1}^{\infty}\frac{1}{n2^{n}}$$

I tried manipulating it to match one of the Important Maclaurin Series and estimate the sum in that fashion but I cannot see to get it to match any.

I was thinking of using $$\sum_{n=1}^{\infty}\frac{\left (\frac{1}{2} \right )^{n}}{n}$$ with the $$\ln\left({1+x}\right)$$ but that only works if its a alternating series.

 

[RLBrown]

ln(2)

Reference

View attachment 4295
with x=2

 

[Pull and Twist]

ln(2)

How did you come to that answer though?

 

[RLBrown]

How did you come to that answer though?

updated w/ref.

 

[Euge]

Hi PullandTwist,

As you know, if $|x| < 1$, $\ln(1 + x)$ has Macluarin expansion

$$\sum_{n = 1}^\infty \frac{(-1)^{n-1}x^n}{n}.$$

So if you set $x = -1/2$, you get

$$\ln(1/2) = \sum_{n = 1}^\infty \frac{(-1)^{n-1}(-1/2)^n}{n} = -\sum_{n = 1}^\infty \frac{(1/2)^n}{n}.$$

Since $\ln(1/2) = -\ln 2$, the result follows.