Amaelle
- 309
- 54
- Homework Statement
- look at the image
- Relevant Equations
- taylor's series
Greetings!
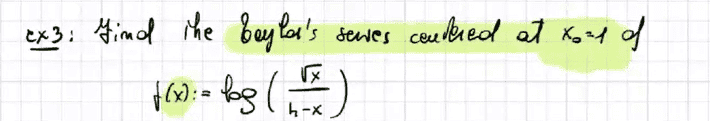
Here is the solution that I understand very well I reach a point I think the Professor has mad a mistake , which I need to confirm
after putting x-1=t
we found:
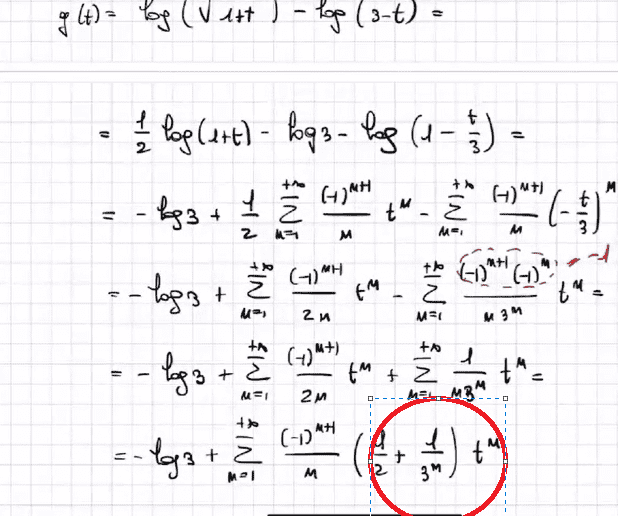
But in this line I think there is error of factorization because we still need and (-1)^(n+1) over 3^n
Thank you!
Best regards!
Here is the solution that I understand very well I reach a point I think the Professor has mad a mistake , which I need to confirm
after putting x-1=t
we found:
But in this line I think there is error of factorization because we still need and (-1)^(n+1) over 3^n
Thank you!
Best regards!