Bounds of the remainder of a Taylor series

[songoku]

Homework Statement

Given that $f(x)=\frac{1}{1+x}$. Find bound of remainder $R_3 (x)$ assuming $|x-1| \leq2$

Relevant Equations

Taylor series

Taylor Inequality

I have found the Taylor series up to 4th derivative:
$$f(x)=\frac{1}{2}-\frac{1}{4}(x-1)+\frac{1}{8}(x-1)^2-\frac{1}{16}(x-1)^3+\frac{1}{32}(x-1)^4$$

Using Taylor Inequality:

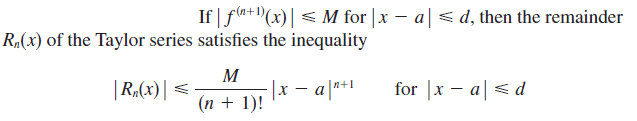$a=1, d=2$ and $f^{4} (x)=\frac{24}{(1+x)^5}$

I need to find M that satisfies $|f^4 (x)| \leq M$

From $|x-1| \leq 2 \rightarrow 0 \leq x+1 \leq 4$ , then $0 \leq (x+1)^5 \leq 4^5$

Putting the boundary of $(1+x)^5$ to $f^{4} (x)$, there is no upper boundary of $f^{4} (x)$ which does not make sense. And actually $x+1$ can not be zero because $f^{4} (x)$ would be undefined so my approach is certainly wrong.

How to find M? Thanks

 

[FactChecker]

For any given $x : |x+1|\le 2$ you can get a bound that is finite.
CORRECTION: Should be $x : |x-1|\le 2$

 

[songoku]

For any given $x : |x+1|\le 2$ you can get a bound that is finite.

I am sorry, but how to get $|x+1|\le 2$?

Thanks

 

[vela]

Putting the boundary of $(1+x)^5$ to $f^{4} (x)$, there is no upper boundary of $f^{4} (x)$ which does not make sense. And actually $x+1$ can not be zero because $f^{4} (x)$ would be undefined so my approach is certainly wrong.

It actually does make sense that you can't find a bound since the function $\frac 1{1+x}$ blows up as $x \to -1$.

 

[songoku]

It actually does make sense that you can't find a bound since the function $\frac 1{1+x}$ blows up as $x \to -1$.

So the answer the question is: no bound for $R_3 (x)$?

Thanks

 

[FactChecker]

I am sorry, but how to get $|x+1|\le 2$?

Thanks

Sorry. I should have said $|x-1|\le 2$, which is given in the problem statement. I will edit my post.

 

[vela]

So the answer the question is: no bound for $R_3 (x)$?

There's no bound on the interval $-1 \le x \le 3$, but is that the interval relevant for calculating the remainder?

 

[songoku]

There's no bound on the interval $-1 \le x \le 3$, but is that the interval relevant for calculating the remainder?

Sorry, that's the only interval I can get. I also have checked the interval of convergence, which is $-1 < x < 3$ and still get no upper bound for $R_3 (x)$. I can't find any other interval related to the question

 

[FactChecker]

Sorry, that's the only interval I can get. I also have checked the interval of convergence, which is $-1 < x < 3$ and still get no upper bound for $R_3 (x)$. I can't find any other interval related to the question

For any particular value $x'$ in (-1,3) we do not care about the entire interval [-1,3]. We only care about $|x-1|\le |x'-1|$. The function derivatives are bounded in that.

 

[songoku]

For any particular value $x'$ in (-1,3) we do not care about the entire interval [-1,3]. We only care about $|x-1|\le |x'-1|$. The function derivatives are bounded in that.

I draw graph of $\frac{24}{(1+x)^5}$

It is monotonically decreasing in interval $-1<x<3$ and the range will be $(\frac{3}{128}, \infty )$

I also draw the graph of $|x-1|$

But sorry I don't understand how to find the interval where $|x-1| \le |x'-1|$

 

[FactChecker]

But sorry I don't understand how to find the interval where $|x-1| \le |x'-1|$

When trying to bound the error of the partial series at a point $x'$, it is only necessary to look at the interval of points $x$ that are at least as close to the 1 as $x'$ is. That is for x in the interval [1-|x'-1|, 1+|x'-1|].

 

[songoku]

When trying to bound the error of the partial series at a point $x'$, it is only necessary to look at the interval of points $x$ that are at least as close to the 1 as $x'$ is. That is for x in the interval [1-|x'-1|, 1+|x'-1|].

So I need to find $M$ where $|f^{3} (x')| \le M$ and $x' \in [a,x]$

$a \le x' \le x \rightarrow 1 \le x' \le 3$ so the value of M is $\frac{3}{4}$

Is this correct? Thanks

 

[FactChecker]

So I need to find $M$ where $|f^{3} (x')| \le M$ and $x' \in [a,x]$

$a \le x' \le x \rightarrow 1 \le x' \le 3$ so the value of M is $\frac{3}{4}$

Is this correct? Thanks

You need to check on both sides of a=1, not just the side that x' is on. I think that we are using different notations, but the idea seems right.

 

[songoku]

I think that we are using different notations

I also think so. Honestly I am still not really understand the notation $|x-1| \le |x'-1|$. I only use Taylor inequality I posted in #1 but after you introduced $x'$, I searched through the web and found this link:

https://brilliant.org/wiki/taylor-series-error-bounds/

This is part of what is in there:

and also

At first, I thought $x$ in $f^{n+1} (x)$ is exactly the same as $x$ in $|x-a| \le d$ but in that link, it is written as $f^{n+1} (z)$ instead where $a<z<x$ so I thought $a$ will always be the lower boundary of $z$, that's why I only checked the value bigger than 1.

You need to check on both sides of a=1, not just the side that x' is on.

By both sides of $a=1$, do you mean for 2 intervals, something like $p<x'<1$ and $1<x'<3$ where $p$ is a value that I need to find first?

Thanks

 

[vela]

You need to check on both sides of a=1, not just the side that x' is on.

Are you sure about this? The Lagrange form of the remainder is
$$R_n(x) = \frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1},$$ where $c$ is between $a$ and $x$. It seems as long as you find an upper bound $M$ for $f^{(n+1)}(c)$ on $(a,x)$ (or $(x,a)$ if $x<a$), you should be fine.

I also think so. Honestly I am still not really understand the notation $|x-1| \le |x'-1|$.

Take $x'$ as fixed. You're finding an upper bound for $R_n(x)$ in the interval $|x-a|<d$ with $d = |x'-a|$.

 

[FactChecker]

Are you sure about this? The Lagrange form of the remainder is
$$R_n(x) = \frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1},$$ where $c$ is between $a$ and $x$. It seems as long as you find an upper bound $M$ for $f^{(n+1)}(c)$ on $(a,x)$ (or $(x,a)$ if $x<a$), you should be fine.Take $x'$ as fixed. You're finding an upper bound for $R_n(x)$ in the interval $|x-a|<d$ with $d = |x'-a|$.

You are proposing that there is a stronger theorem about the bound on the error. I am not aware of it.
CORRECTION: Apparently there is a stronger theorem. It is referenced in @songoku 's post #14)

 

[songoku]

Take $x'$ as fixed. You're finding an upper bound for $R_n(x)$ in the interval $|x-a|<d$ with $d = |x'-a|$.

I will try to use that:

$$d=|x'-a|$$
$$2=|x'-1|$$
$$x'=3 ~\text{or} ~x'=-1$$

Since $x' \in (a,x)$ or $x' \in (x,a)$, there will be 2 intervals, which are $-1 < x' < 1$ or $1 < x' < 3$. No upper bound for the remainder in interval $-1 <x'<1$ so the one I should use is $1<x'<3$

Is this correct? Thanks

 

[Mark44]

I've deleted a couple of my posts and replies to them, as I really misread the graph in post #10. As a result, my responses didn't add anything to the thread.

 

[vela]

Is this correct? Thanks

No.

Say you want to find an upper bound for $R_3(1.5)$, i.e., $x'=1.5$. The remainder is equal to
$$R_3(1.5) = \frac {f''''(c)}{4!} (1.5-1)^4$$ for some $c$ in the interval $(1,1.5)$. If you find an upper bound $M$ for $f''''(x)$ on the interval $(1,1.5)$, then you can say
$$R_3(1.5) \le \frac {M}{4!} (1.5-1)^4.$$ Note that you don't really care that the series converges between $-1 < x \le 3$ to find an upper bound for the remainder $R_3(1.5)$.

 

[songoku]

No.

Say you want to find an upper bound for $R_3(1.5)$, i.e., $x'=1.5$. The remainder is equal to
$$R_3(1.5) = \frac {f''''(c)}{4!} (1.5-1)^4$$ for some $c$ in the interval $(1,1.5)$. If you find an upper bound $M$ for $f''''(x)$ on the interval $(1,1.5)$, then you can say
$$R_3(1.5) \le \frac {M}{4!} (1.5-1)^4.$$ Note that you don't really care that the series converges between $-1 < x \le 3$ to find an upper bound for the remainder $R_3(1.5)$.

Let me try again:

I want to find an upper bound for $R_3(x)$. The remainder is equal to
$$R_3(x) = \frac {f''''(c)}{4!} (x-1)^4$$ for some $c$ in the interval $(1,x)$ or $(x,1)$. There will be 2 intervals since I do not know whether $x>1$ or $x<1$

From the question: $|x-1| \le 2$ so $-1 \le x \le 3$

Then how to proceed to find the relevant interval for the remainder? Thanks

 

[haruspex]

how to proceed to find the relevant interval for the remainder?

If I understand the question, it can be any interval containing x and 1. So for x<1 you can choose [x,1).

 

[songoku]

If I understand the question, it can be any interval containing x and 1. So for x<1 you can choose [x,1).

So for $x<1$ the interval is $[x,1)$ and for $x>1$ the interval is $(1,x]$.

Then how to find the upper bound? Thanks

 

[haruspex]

So for $x<1$ the interval is $[x,1)$ and for $x>1$ the interval is $(1,x]$.

Then how to find the upper bound? Thanks

Is there a local extremum within the interval? What about values at the ends of the interval?

 

[songoku]

Is there a local extremum within the interval? What about values at the ends of the interval?

Since $\frac{24}{(1+x)^5}$ is monotonically decreasing in interval $-1<x \le 3$, there is no local extremum so the upper bound will the located at the left end-point of the interval.

I think I only need to find upper bound either on $[x,1)$ or $(1,x]$ so the one I can use is $(1,x]$. The upper bound will be $\frac 3 4$

Is this correct? Thanks

 

[FactChecker]

Since $\frac{24}{(1+x)^5}$ is monotonically decreasing in interval $-1<x \le 3$, there is no local extremum so the upper bound will the located at the left end-point of the interval.

I think I only need to find upper bound either on $[x,1)$ or $(1,x]$ so the one I can use is $(1,x]$. The upper bound will be $\frac 3 4$

Is this correct? Thanks

You should find a separate bound for the two cases, depending on where x is. And remember that the original problem was to find the bounds, not just the upper bound. So you may need to calculate a maximum and a minimum. (They might all have the same magnitude, but they might not in all example problems.)

 

[songoku]

You should find a separate bound for the two cases, depending on where x is. And remember that the original problem was to find the bounds, not just the upper bound. So you may need to calculate a maximum and a minimum. (They might all have the same magnitude, but they might not in all example problems.)

For $[x,1)$ the upper bound will be $\frac{24}{(1+x)^5}$ and lower bound is $\frac 3 4$

For $(1,x]$ the upper bound will be $\frac{3}{4}$ and lower bound will be $\frac{24}{(1+x)^5}$

Is this correct? Thanks

 

[FactChecker]

Looks ok to me.

 

[songoku]

Thank you very much for the help and explanation FactChecker, vela, Mark44, haruspex