shayaan_musta
- 208
- 2
Hello experts,
I have attached the figure below kindly see it. And here is my calculation,
Using law of sine,
from figure we can say that α+β=120°
and β=120°-α
and sin(β)/sin(α)=PA/PB=3/40=0.075
so,
sin(120°-α)=sin(120°)cos(α)-cos(120°)sin(α)
since, sin(β)=sin(120°-α)
so,
sin(β)=sin(120°)cos(α)-cos(120°)sin(α)
dividing both sides by sin(α)
so,
sin(β)/sin(α)=sin(120°)cos(α)/sin(α)-cos(120°)sin(α)/sin(α)
sin(β)/sin(α)=sin(120°)cos(α)/sin(α)-cos(120°)
sin(β)/sin(α)=0.866*cos(α)/sin(α)-(-0.5)
3/40=0.866*cot(α)+0.5
0.075=0.866*cot(α)+0.5
-0.425=0.866*cot(α)
cot(α)=-0.425/0.866
cot(α)=-0.49
α=-63.86°
What is this? Why α is -ve? Where I have gone wrong? From figure we can clearly see that it is more than 90°. But calculation says it is -63.86°.
According to the book point A is at -3.70 and B is at -53.35. But I am not getting my angle correct. HElp
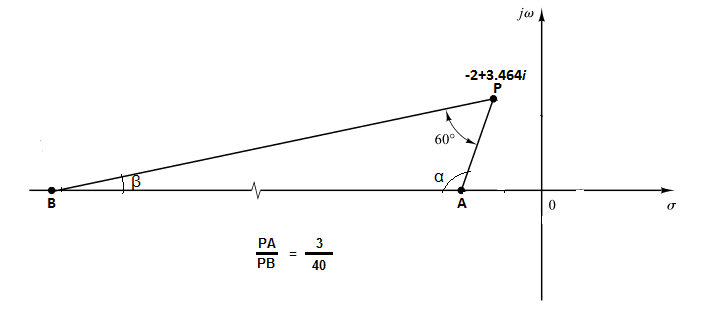
I have attached the figure below kindly see it. And here is my calculation,
Using law of sine,
from figure we can say that α+β=120°
and β=120°-α
and sin(β)/sin(α)=PA/PB=3/40=0.075
so,
sin(120°-α)=sin(120°)cos(α)-cos(120°)sin(α)
since, sin(β)=sin(120°-α)
so,
sin(β)=sin(120°)cos(α)-cos(120°)sin(α)
dividing both sides by sin(α)
so,
sin(β)/sin(α)=sin(120°)cos(α)/sin(α)-cos(120°)sin(α)/sin(α)
sin(β)/sin(α)=sin(120°)cos(α)/sin(α)-cos(120°)
sin(β)/sin(α)=0.866*cos(α)/sin(α)-(-0.5)
3/40=0.866*cot(α)+0.5
0.075=0.866*cot(α)+0.5
-0.425=0.866*cot(α)
cot(α)=-0.425/0.866
cot(α)=-0.49
α=-63.86°
What is this? Why α is -ve? Where I have gone wrong? From figure we can clearly see that it is more than 90°. But calculation says it is -63.86°.
According to the book point A is at -3.70 and B is at -53.35. But I am not getting my angle correct. HElp