Finding the y axis on a probability density graph

[Sorin2225]

Homework Statement

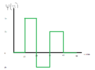
I was given a probability density graph and from it I had to figure out what B was in nm^-1/2

Relevant Equations

I think it's just from the graph.

I assumed to find it I would need to find the area under the graph. I also assumed that the part under x would cancel out so I would be left with 2b*10=1 if it was, in fact, true that it had to equal to one. So my final answer was (1/10)/2 nm^-1 but the actual answer was 0.0845 nm^-1/2 and I'm unsure of how this answer was gained.

 

[RPinPA]

That is not a probability density. A probability density can not be negative.

Judging by the use of the symbol $\psi$ I'm guessing this is a quantum mechanical wavefunction, so the actual probability density is $|\psi|^2$. Your method was correct, that the total probability (total area) must be 1. So make that change and see how it works out.

The units of $b$ are another clue that you're supposed to be squaring these values to get the density, because $b^2 \times$ [length] is unitless.

 

[Sorin2225]

To get b however I'm doing 3b*10-2b*10+2b*10=1 and rearranging for this but I'm nowhere near the right answer

 

[RPinPA]

To get b however I'm doing 3b*10-2b*10+2b*10=1

You shouldn't be. You're integrating $\psi$ with respect to $x$ and I just told you that $\psi$ is not the probability density, not the thing you should be integrating. Therefore trying to get a total probability of 1 by integrating $\psi$ is not a correct thing to do.

Again, you want to integrate the probability density. $\psi$ is not the probability density. Find the probability density and then integrate that.

I know you started from this assumption, in your original post:

I was given a probability density graph...

but what I'm trying to say is that you were not given a probability density graph. A probability density can not be negative. $\psi$ is by inspection not a probability density.

 

[Sorin2225]

Yes sorry, I realized that my initial assumption about the type of graph was wrong. I am confused on how I am meant to be changing the probability into probability density. To do this I attempted
to square the probability