Finding the z component of vectors that form a triangle?

[rockchalk1312]

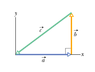
For the vectors in the figure, with a = 1.1 and b = 2.6, what are (a) the z component of a x b, (b) the z component of a x c, and (c) the z component of b x c?


Everything I've tried to look up involves vectors that are in unit notation, etc. I just don't understand how to do it when all you have for the vector is one number.

 

[ap123]

With the information given, you can work out the angle between a and c.
Then use the formula for the cross product which uses the magnitudes and angle.

 

[rockchalk1312]

With the information given, you can work out the angle between a and c.
Then use the formula for the cross product which uses the magnitudes and angle.

So using a x b = |a| |b| sinθ told me that the z component of a x b = (1.1)(2.6)sin90 = 2.9.

And for b x c = (2.6)(2.823)sin(90-67.07)=2.9.

These were both correct, but then when I tried to do a x c = (1.1)(2.823)sin67.06 = 2.9 this was the wrong answer.

Am I missing something completely obvious?

Thank you for your help!

 

[haruspex]

So using a x b = |a| |b| sinθ

That should be |a x b| = |a| |b| sinθ. If you want a x b, not just its magnitude, you need to worry about direction. Yes, it's in the z direction, but is it positive or negative? You need to apply the convention for a x b (as distinct from b x a) to determine that.
From the diagram, you have a + b + c = 0. So 0 = a x (a + b + c) = a x a + a x b + a x c = a x b + a x c. It follows that a x b and a x c must have opposite signs.

 

[rockchalk1312]

Yes, it's in the z direction, but is it positive or negative?

Perfect THANK you that was certainly what I was missing.