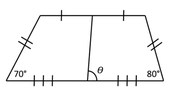
Let $a,b,O,A,B,M$ as in the following picture ($O$ is the origin).
\begin{tikzpicture}
\def\a{4}
\def\b{4}
\draw[fill=black] (-\a,0) -- node[below] {a} (0,0) node[below] {O} -- node[below] {a} (\a,0);
\draw (-\a,0) node[above right] {$70^\circ$} -- node
{b} +(70:\b) coordinate (A) node[above] {A};
\draw (\a,0) node[above left] {$80^\circ$} -- node
{b} +({180-80}:\b) coordinate (B) node[above] {B};
\draw (A) -- (B);
\draw[fill=black] (0,0) -- +(85:{\b*sin(75)}) node[above] {M};
\draw[thick] (0,0) node[above right] {$\theta$} +(.6,0) arc (0:85:.6);
\end{tikzpicture}
Then the coordinates of A are $(-a+b\cos 70^\circ, b\sin 70^\circ)$.
And the coordinates of B are $(a-b\cos 80^\circ, b\sin 80^\circ)$.
Point M is the average of A and B, which is:
$$M = \left(\frac b2(\cos 70^\circ - \cos 80^\circ), \frac b2(\sin 70^\circ+\sin 80^\circ)\right)$$
Using the sum and difference formulas of sine and cosine, we get:
$$M = b(\sin 75^\circ \sin 5^\circ, \sin 75^\circ \cos 5^\circ)$$
And with the complement rule:
$$M = b\sin 75^\circ (\cos 85^\circ, \sin 85^\circ)$$
Thus $\theta = 85^\circ$.