Finding this constant in a quartic polynomial

[chwala]

Homework Statement

find the set of values of $k$ for which the equation
$3x^4+4x^3-12x^2+k =0$ has 4 real roots

Relevant Equations

quartic polynomials

$x^2(3x^2+4x-12) +k=0$
$(3x^2+4x-12)= \frac{-k}{x^2}$

or

$(4x^3-12x^2)=-k-3x^4$
$4(3x^2-x^3)=3x^4+k$
$4x^2(3-x)= 3x^4+k$

or using turning points,

let $f(x)= 3x^4+4x^3-12x^2+k$
it follows that,
$f'(x)=12x^3+12x^2-24x=0$
$12x(x^2+x-2)=0$
$12x(x-1)(x+2)=0$ the turning points for this graph are at,
$x=0$, $x=1$ & $x=-2$

or considering the first term and the constant, we have
$(ax+k=0)$, where $a=3$, possible values for $k = ±1, ±3...$

 

[etotheipi]

The easiest way to do it would be to sketch the graph at the two limiting cases for 4 solutions and then determine what $k$ has to be.

 

[chwala]

on my last equation, both sides are satisfied with $x=1, k=5$

 

[etotheipi]

The set of values that $k$ can take is a real interval. You can work out the relative $y$ coordinates of all of the turning points and then consider the critical cases.

 

[chwala]

show me how...

 

[etotheipi]

Well the coordinates of the turning points for some arbitrarily chosen value of $k$ are $(-2, -32+k)$, $(0, k)$ and $(1, -5+k)$. Evidently the maximum in the middle has the highest $y$ coordinate, followed by the minimum on the right and finally by the minimum on the left which is the lowest.

By varying the value of $k$, you are essentially just translating the graph vertically. For $4$ solutions, you want the $x$ axis to cut the curve $4$ times. So considering one or two graphs should allow you to determine the critical values of $k$.

 

[chwala]

will i be right to state that the domain of $x$ in my last solution should satisfy $x<3$?

 

[chwala]

Well the coordinates of the turning points for some arbitrarily chosen value of $k$ are $(-2, -32+k)$, $(0, k)$ and $(1, -5+k)$. Evidently the maximum in the middle has the highest $y$ coordinate, followed by the minimum on the right and finally by the minimum on the left which is the lowest.

By varying the value of $k$, you are essentially just translating the graph vertically. For $4$ solutions, you want the $x$ axis to cut the curve $4$ times. So by considering one or two graphs should allow you to determine the critical values of $k$.

i had tried that approach earlier...let me see

 

[chwala]

i think i got it just a minute... the answer is $0<k<5$. Is there not an algebraic way of finding these set of values?
For $k=5$ we get three critical values. I did not want to post all the graphs here, ...the graph posted here is for $k=1$...

 

[etotheipi]

Is there not an algebraic way of finding these set of values?

I've no idea actually. There does exist a quartic discriminant but that is positive if all four roots are real or if all four roots are complex, so it doesn't really help.

Perhaps someone else knows an algebraic method... we'll have to wait and see!

 

[ehild]

i think i got it just a minute... the answer is $0<k<5$. Is there not an algebraic way of finding these set of values?

The function f(x)=3x^4 +4x^3 - 12x^2+ k=0 has minima at x=-2 and at x=1, and a maximum at x=0.
You need to choose k, so as the minimum values of f(x) are negative, the maximum value is positive. Substituting the x values of the turning points into the function, you get the range of k where the conditions f(-2)<0, f(1)<0 and f(0)>0
Moreover, you need to exclude multiple roots.

 

[epenguin]

You got the turning points. I suggest you sketch or graph the function for k = 0.

That, as it happens, already tells you something. Now what happens to the graph as from 0 you increase or decrease k?

And doesn't that tell you what little else you need to know? (Though you seem to have stumbled on it already.)

(As extra flourish, it would take little to also say for what k do you get two and for what k zero real roots.)

 

[haruspex]

Think about the boundaries of the ranges of k. What can you say about the number and nature of solutions at one of these boundaries? Does that suggest a way to find one of the roots at each?

 

[chwala]

haruspex appreciated, i understand the behavior of the function when varying the values of $x$ between the three turning points.
The approach mentioned by epenguin makes a lot of sense to me, as one would be able to say, tell the behavior of the curve in terms of gradient values( changing from either positive to negative...), in reference to the turning points that i found.
In post $9$ i was able to use desmos graphing tool to see the behaviour of the graph...i did not want to post all the graphs here...i can see why the solution of the set values is in the region $0<k<5$.

 

[haruspex]

haruspex appreciated, i understand the behavior of the function when varying the values of $x$ between the three turning points.
The approach mentioned by epenguin makes a lot of sense to me, as one would be able to say, tell the behavior of the curve in terms of gradient values( changing from either positive to negative...), in reference to the turning points that i found.
In post $9$ i was able to use desmos graphing tool to see the behaviour of the graph...i did not want to post all the graphs here...i can see why the solution of the set values is in the region $0<k<5$.

Yes, I think the two approaches are the same. I was thinking in terms of repeated roots, but of course they are the turning points.
But the repeated roots approach also works for something like $3x^4+4x^3-kx^2+1=0$.

 

[epenguin]

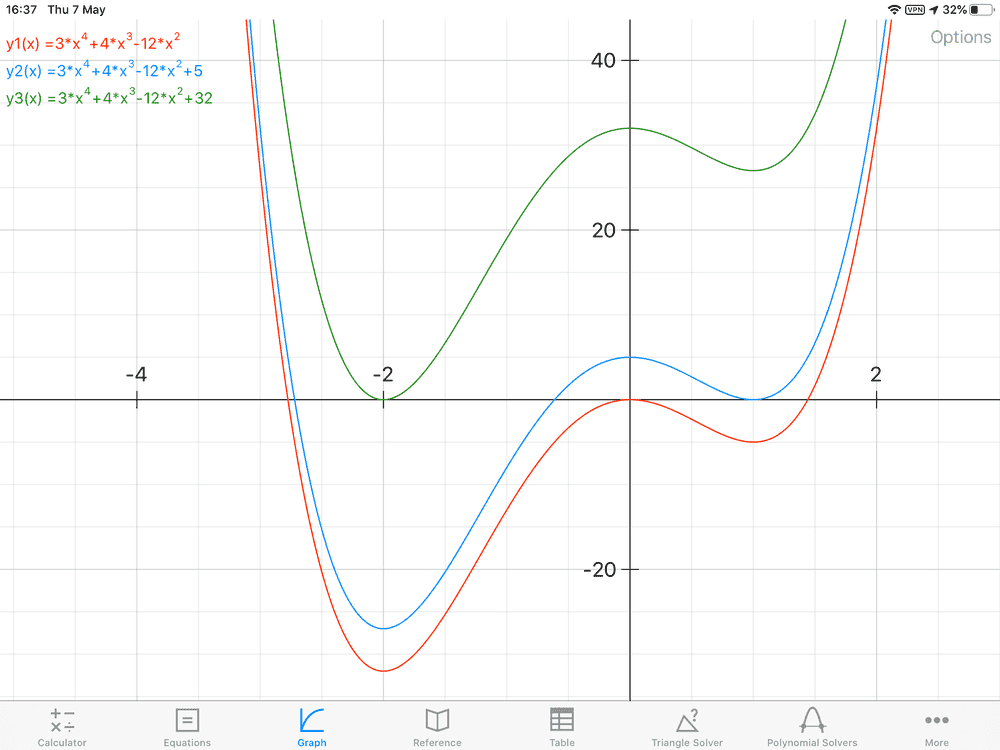
Surely it did not require very much to find out as well as 0 < k < 5 giving four real roots, k < 0 and 5 < k < 32 give two real roots and k > 32 gives zero real roots while if any of those inequalities are equalities, then there are two coincident roots. In no case are there four coincident roots.

i think i got it just a minute... the answer is $0<k<5$. Is there not an algebraic way of finding these set of values?

I've no idea actually. There does exist a quartic discriminant but that is positive if all four roots are real or if all four roots are complex, so it doesn't really help.

Perhaps someone else knows an algebraic method... we'll have to wait and see!

This is a good question. One would like to know if any proof, argument, solution etc can be made on more minimal assumptions, or anyway if a certain different method can be used. Perhaps without using calculus and derivatives?

Maybe this sort of thing? The discriminant of the given polynomial is (with an irrelevant numerical factor removed)

$$ =k\left( k^{2}-37k+160\right) =k\left( k-5\right) \left( k-32\right)$$

That does give you the values as asked. It needs a bit more to know whether the ranges where it is negative give four or zero real roots, as mentioned by etothepi.

But against this it is a pain to calculate 5 x 5 determinant, even one with a number of zeros and units. I started, for the hell of it, but decided I shoudn't waste my time or encourage anyone else to waste theirs, so used WolframALpha to do it. Then it would be not too difficult to factorise – however we actually already knew the numerical values of its roots!

However you may be thinking, ah, but it is purely algebraic whereas other methods talk about the derivative, i.e. involve calculus. Firstly let me say that one definition of the discriminant is the condition that a root of the polynomial equal a root of its derivative. at least, that is how you most easily get the formula (like the determinant above) for the discriminant so we haven't got away from derivatives. Still (now I think of it) you could argue from a different definition, that it is the product of all squares of differences between roots, which leads with more difficulty to the same formula. Anyway you will find all the algebra texts on the subject of the nature or localisation of roots, use derivatives very freely, and a great deal.But the clinching thing is that derivatives of polynomials don't have to be a calculus concept - they can be defined purely algebraically! So they are in my Bible (Old Testament) of algebraic equations*. I don't know whether this is common in other texts - you might easily miss it because you tend to rush cursorily over stuff one imagines one knows already - I know I did on first reading of Burnside & Panton. So it sounds like a good question, but I think at the end of the day there is nothing in it really. You best get the answers to this question just moving the curve up and down.

*The Theory of Equations, Burnside & Panton, 7th ed. 1912.