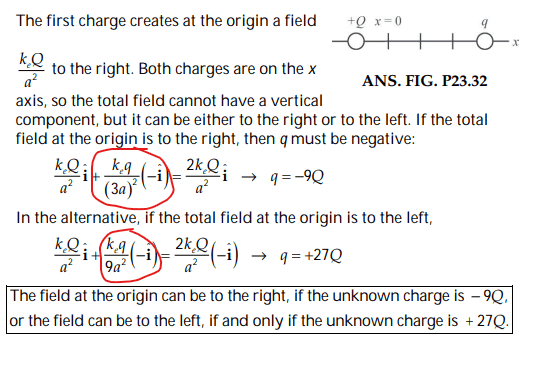SUMMARY
The discussion centers on the behavior of electric fields produced by point charges, specifically addressing the direction of the electric field generated by a charge denoted as q. It is established that if charge q is positive, the electric field at the origin points to the left, while if q is negative, the electric field points to the right. This conclusion is based on the fundamental principles of electrostatics, where the direction of the electric field is determined by the nature of the charge.
PREREQUISITES
- Understanding of electric fields and point charges
- Knowledge of Coulomb's Law
- Familiarity with the concept of test charges
- Basic principles of electrostatics
NEXT STEPS
- Study the implications of Coulomb's Law on electric field direction
- Explore the concept of superposition in electric fields
- Learn about electric field lines and their representation
- Investigate the behavior of electric fields in different charge configurations
USEFUL FOR
Students studying physics, educators teaching electrostatics, and anyone interested in understanding the principles of electric fields and charge interactions.