Finding velocity of car in Carnival ride

[chicagobears34]

Homework Statement

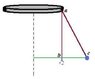
You've taken your neighbor's young child to the carnival to ride the rides. She wants to ride The Rocket. Eight rocket-shaped cars hang by chains from the outside edge of a large steel disk. A vertical axle through the center of the ride turns the disk, causing the cars to revolve in a circle. You've just finished taking physics, so you decide to figure out the speed of the cars while you wait. You estimate that the disk is 6m in diameter and the chains are 6m long. The ride takes 10s to reach full speed, then the cars swing out until the chains are 30degrees from vertical.

Homework Equations

Fc=m(v^2)/r
w=mg

The Attempt at a Solution

I summed the Forces in the Y direction, so 0=Ft*cos30 -mg
Ft being the tension force on the cable of the car
Ft=mg/cos30
2nd equation: Ft*sin30 -Fc
Fc=Ft*sin30
sub in mv^2/r for Fc
solved for v and i got v=sqrt(r*g*tan30)
i plugged in the radius of the disk which is 3m and gravity which is 9.81m/s^2
v=4.122m/s^2, but that was wrong
What am I doing wrong?

 

[PhanthomJay]

The radius of the cars circle is not the same as the disc radius.

 

[TSny]

solved for v and i got v=sqrt(r*g*tan30)
i plugged in the radius of the disk which is 3m and gravity which is 9.81m/s^2

Careful. Are you sure r is the radius of the disk?

 

[chicagobears34]

if I do radius as 9m then I get 7.14m/s as the velocity, which is wrong also

 

[PhanthomJay]

You are not calculating the radius correctly. Recheck your geometry and trig for the swing angle

 

[chicagobears34]

You are not calculating the radius correctly. Recheck your geometry and trig for the swing angle

ok how would I go about calculating it properly, I have no idea

 

[TSny]

Draw a side view of the disk. Draw the car hanging vertically (before the ride starts). On the same figure draw the car hanging from the same point at 30 degrees from the vertical (after the ride starts). Draw a line representing the radius of the circle that the car is traveling in. Can you see how to determine the value of the radius?

 

[chicagobears34]

well doesn't it make a 30 60 90 triangle?
so the radius would be 3+(2*9/root3)?

 

[TSny]

well doesn't it make a 30 60 90 triangle?

Yes.

so the radius would be 3+(2*9/root3)?

The expression in the parentheses is incorrect. Which side of the 30 60 90 triangle represents the additional amount you need to add to the 3 m radius of the disk? What is the length of the hypotenuse of the triangle?

 

[chicagobears34]

the hypotenuse would be the length i need to add by 3. so it should be 3+(2*6/root3)
because the side opposite of the 60 degree angle is a*root3 and the hypotenuse is 2a.

 

[TSny]

Is your diagram similar to the attached figure? If so, what is the length of the hypotenuse of the triangle a b c?