- #1
fawk3s
- 342
- 1
Homework Statement
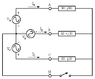
http://img268.imageshack.us/img268/8981/71713784.png
http://img268.imageshack.us/img268/8981/71713784.png
In a 3-phase circuit, the switch SA is opened, disconnecting the grounding wire. Due to the powerful generator, the voltage between phases remains the same - 400 V. The impedances are given. Find all the missing voltages/currents.
The Attempt at a Solution
First of all, as the voltage between the phases remains the same, that means that when the grounding wire was connected, the voltages in the phases were 400/sqrt3=231 V
The problem I am having here is finding the voltages. If those were given, it would be rather easy to find the rest. I usually tend to solve these by using the vector diagram and solving the given triangles (I don't know is this is the proper way to do it, but so far it has given me right answers).
Now that we are only given the impedances and the voltage between phases, it leads me to believe that we are supposed to find the currents first, and then find the voltages by multiplying the found currents and impedances. But I am not really sure on how to find them.
I tried adding the according impedances together: Za+Zb and then Za+Zc. Then find the currents which which go from A>B and A>C (as the voltages between both of them is 400 V.) Then add the A>B and A>C vectors together to find Ia.
This seems to be incorrect though, giving me answers off by about 0.3-0.5 A.
So why didnt this way work? How to approach the problem?
And what exactly causes the voltages to change when the grounding wire is disconnected?
Thanks in advance
Last edited by a moderator: