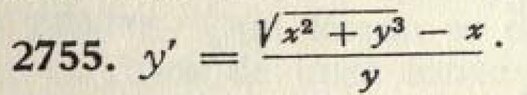Discussion Overview
The discussion revolves around a first-order nonlinear ordinary differential equation (ODE) presented in Demidovitch's book. Participants explore various methods for solving the equation, including transformations to polar coordinates, and discuss the implications of different approaches and substitutions.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants inquire about the specific tasks related to the differential equation, such as finding steady-states or plotting the vector field.
- Several participants express skepticism about the utility of polar coordinates for the given equation, particularly due to its asymmetry.
- One participant, Dan, reports unsuccessful attempts to solve the equation using various substitutions and mentions that Mathematica could not provide a closed-form solution, suggesting numerical methods may be necessary.
- Another participant mentions a possible typo in the original problem, proposing an alternative form of the equation that could simplify the analysis when using polar coordinates.
- Some participants explore the substitution \( v = \frac{y}{x} \) and express difficulty in progressing towards a solution, with one participant noting the complexity of the square root in series expansion attempts.
- Another participant provides a detailed transformation to polar coordinates, showing steps that lead to a potential solution involving \( y^2 = 2Cx + C^2 \).
- One participant suggests that the transformation to polar coordinates simplifies the ODE significantly, leading to a straightforward result.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the best approach to solve the differential equation. There are competing views on the effectiveness of polar coordinates and the validity of the original problem statement.
Contextual Notes
Participants note limitations in their approaches, including unresolved mathematical steps and the complexity introduced by the square root in the equation. The discussion reflects a variety of methods attempted without a definitive resolution.