MisterH
- 12
- 0
- TL;DR
- Find a fitness function such that: filter(LWMA-EMA) is in-phase with the sinusoid it's placed on, not by correlation, but calculated on filter weights * segment of sinusoid (that has a length equal to the filter weights), so on only 1 step of the convolution.
Fitness function for window length of filter
On a sinusoidal signal with amplitude 1, and period P, an exponential moving average (EMA) (with alpha = 1/n), and a linear weighted moving average (LWMA) (with window length n) are calculated; when you subtract the EMA from the LWMA, it can be seen that the difference of these 2 filters will be in phase with the sinusoid when the window length n of the LWMA = P/4 (and for the EMA alpha = 1/n). So if P=40, the signal: LWMA(wave,10)-EMA(wave,0.1) is in phase with the wave, but at lower amplitude. The weight function of this "difference filter" looks like this:
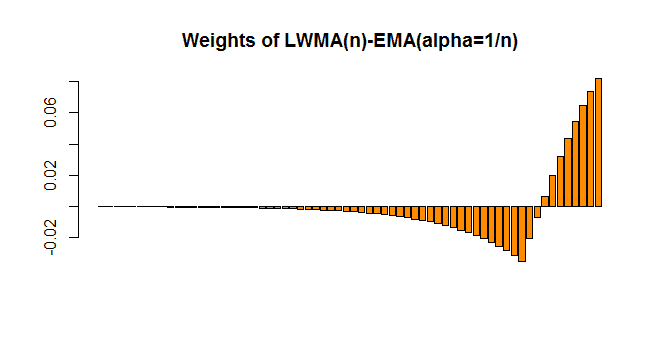
Similar, but not equal to the weights of a "zero-lag exponential moving average". It can be seen that the correlation (degree of linear association) between the wave and the filter will be maximal at n = P/4:

Now, my question is: instead of looking at an entire wave, can you just look at the data in the window, multiplied with the filter weights to find which window length n will result in a signal that is in phase with the sinusoid? e.g.:
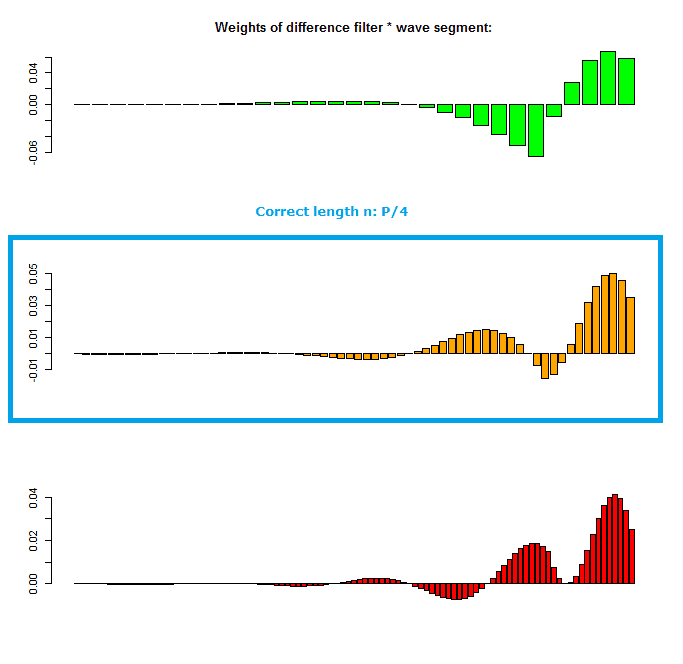
So at e.g. point x, wave[(x-n+1):x] is multiplied with the weight function of the difference filter, on this data, some sort of calculation is made, that returns a value e.g. between 0 and 1, with a maximum for n = P/4? So the fitness of window length n1: wave[(x-n1+1):x]*weightfunction(n1) can be compared with the fitness of window length n2: wave[(x-n2+1):x]*weightfunction(n2), and the one where n equals a -previously unknown- P/4 will return a maximum for this fitness/error function.
How would you create such a fitness function? Could it be related to curvature, or some sort of exponential fit, or some property of sinusoids?
All input is welcome and appreciated.
On a sinusoidal signal with amplitude 1, and period P, an exponential moving average (EMA) (with alpha = 1/n), and a linear weighted moving average (LWMA) (with window length n) are calculated; when you subtract the EMA from the LWMA, it can be seen that the difference of these 2 filters will be in phase with the sinusoid when the window length n of the LWMA = P/4 (and for the EMA alpha = 1/n). So if P=40, the signal: LWMA(wave,10)-EMA(wave,0.1) is in phase with the wave, but at lower amplitude. The weight function of this "difference filter" looks like this:
Similar, but not equal to the weights of a "zero-lag exponential moving average". It can be seen that the correlation (degree of linear association) between the wave and the filter will be maximal at n = P/4:
Now, my question is: instead of looking at an entire wave, can you just look at the data in the window, multiplied with the filter weights to find which window length n will result in a signal that is in phase with the sinusoid? e.g.:
So at e.g. point x, wave[(x-n+1):x] is multiplied with the weight function of the difference filter, on this data, some sort of calculation is made, that returns a value e.g. between 0 and 1, with a maximum for n = P/4? So the fitness of window length n1: wave[(x-n1+1):x]*weightfunction(n1) can be compared with the fitness of window length n2: wave[(x-n2+1):x]*weightfunction(n2), and the one where n equals a -previously unknown- P/4 will return a maximum for this fitness/error function.
How would you create such a fitness function? Could it be related to curvature, or some sort of exponential fit, or some property of sinusoids?
All input is welcome and appreciated.