+
View attachment 351572
Start with this, and you'll see how it develops.
Apply "Energy Equation" from fluid mechanics for an incompressible flow in the network :
$$ \frac{P}{\gamma} + Z +\frac{V^2}{2g} + h_p = \frac{p}{\gamma} + z +\frac{v^2}{2g} + \sum {h_l} $$
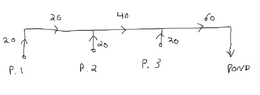
Branch ##1## to ##a## is in parallel with ##2## to ##a## (or the head of pump 2 ##h_p## in this case), and both in series with head loss from ##a## to ##b##.
##k## in the diagram generically characterizes the head loss.
Pretend it's a constant independent of flow velocity for now i.e. ##h_l = k\frac{u^2}{2g}##
You have to satisfy the energy equation at/between nodes, so we have to apply the equation above around the system.
If you have questions about the notation I just conjured (being lazy), ask.
Considering a system without losses is pretty much a waste here IMHO (in the cases dealing with applications of pumps). I can push whatever flow I want through a needle at no pressure if it's over idealized. Reality is quite different.