Flux in a Uniform Magnetic Field

[Cardinalmont]

Thank you for reading my post. I was thinking about induced emf and magnetic flux and I realized I have a huge misunderstanding, but I don't know exactly what it is. Below I will list 4 statements which I logically know cannot all be simultaneously true. Can you please tell me which one(s) are incorrect in order to aid my understanding?

1. In order to create an emf in a conductor there must be a change in magnetic flux.
This can be seen by ε=NΔΦ/Δt, If ΔΦ=0 then so will ε

2. Magnetic flux is equal to the product of a conductor's surface area, magnetic field passing through that surface area, and the angle between the two. This is given by Φ=B⋅A

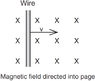
3 When a wire moves through a uniform magnetic field, neither its surface area, nor the strength of the magnetic field, nor the angle between the two are changing ∴ change in magnetic flux = 0 ∴ There is no induced emf.

4 When a wire moves through a uniform magnetic field, an electromagnetic force will force electrons in the wire to one side inducing an emf.

It is clear to see that points 3 and 4 are in direct contradiction of each other. I believe 3 is false, but I can't see the logical flaw! Please help me!

Thank you.

 

[Charles Link]

Number 3 is incorrect because the wire can be considered to be part of the boundary of a surface in the rest frame of the magnetic field, and the area of that surface is changing. The EMF turns out to be $\mathcal{E}=vBL$. This topic was addressed in great detail in a recent Insights article by @vanhees71 , https://www.physicsforums.com/insights/homopolar-generator-analytical-example/ , but if you are a first or second year physics student, you probably don't need to understand the full detail.

 

[Hydrous Caperilla]

Number 3 is incorrect.It is a type of motional emf

 

[vanhees71]

It's also good to think about such problems not only in terms of Faraday's law but also in terms of electromagnetic interactions. In case 3 you have a wire, which you can see as a container of the gas of conduction electrons. Now moving through the magnetc field $\vec{B}$ leads to the force $\vec{F}_1=q \vec{v} \times \vec{B}/c$ an each electron with charge $q(=-e)$. That implies that the electrons move towards one end of the wire (and are lacking at the other end). Thus an electric field is built up, leading to a force $\vec{F}_2=q \vec{E}$. The stationary state is reached, as soon as the total force on the electrons is 0. Putting the two expressions for the forces together leads to the result given in #2.

 

[Cardinalmont]

Thank you everyone! I figured out where my misunderstanding was sprouting from.
As I stated before, in the equation Φ=B⋅A, A is the surface area of the conductor.
My misunderstanding was of the bounds of each term in Φ=B⋅A

When looking at a specific area in the magnetic field, before the wire has moved into that area the value a A for that specific space is 0 because there is no conductor there. As the wire moves into the space then there begins to be an increasing and then decreasing value of A for that specific space thus resulting in a change in flux for that specific space, and an induced emf.