palaphys
- 266
- 17
- Homework Statement
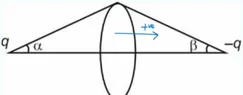
- two charges +q and -q are placed on the axis of a ring at a distance 16cm and 9cm from the center on opposite sides. the ring has a charge 2q uniformly distributed on it. find the flux through the ring.
- Relevant Equations
- solid angle, gauss law
here is a simple diagram representing this situation. The issue I'm facing with this problem is a matter of sign convention.
We can write the flux through the ring as the sum of the contribution of fluxes due to the point charges individually.
So $$\Phi_{\text{net}} = \Phi_{+q} + \Phi_{-q} $$
additionally I was able to calculate the magnitudes of both of the individual fluxes as
## \left| \Phi_{+q} \right| = \frac{q}{10 \epsilon_0} ##
and
## \left| \Phi_{-q} \right| = 2\frac{q}{10 \epsilon_0} ##
both using a basic approach with solid angles(relating half angle to solid angle).but to get the net flux, should I add both the fluxes, or subtract them?
edit- radius of the ring is given as 12cm
Last edited: