Force and Motion rod tension problem

[KingKai]

Homework Statement

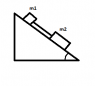
A box of ant aunts (m₁ = 1.65kg ) and a box of ant uncles (m₂ = 3.30 kg) slide down an inclined plane while attached by a massless rod parallel to the plane. The angle of incline θ = 30°. The coefficient of kinetic friction between the aunt box and the incline is μ₁ = 0.226; that between the uncle box and the incline is μ₂ = 0.113.

m1 is above m2 on the incline.

Compute: a)The tension in the rod
b)The magnitude of the common acceleration of the two boxes

Bonus: How would the the answers to a) and b) differ if the uncles trailed the aunts?

Homework Equations

F = ma

Fn = mgcosθ

Fp = mgsinθ

Ff = μFn

The Attempt at a Solution

F = idk...

 

[Doc Al]

What forces act on each box? Apply ƩF = ma.

 

[KingKai]

Could you be any more vague..


This is what I don't understand: How to I add up the tension vectors to get a resultant tension in the rod?

 

[howie8594]

You have to find the acceleration of the system to find the tension. Now, the only reason there would be any tension is if the boxes have different coefficients of friction because otherwise, they would accelerate at the same pace down the ramp without help from a cord. It would be like dropping two masses connected by a string off a cliff. They'd both accelerate at the same rate and there wouldn't be tension in the string. So first you have to find the force acting parallel to the hill for each block individually. That includes adding the force down the hill and the friction acting against it for each block. Once you have the accelerations for both blocks (how they would accelerate without the rope there), you can find the net force for each one. You subtract the first force from the second, you get the tension.

 

[Doc Al]

Could you be any more vague..

LOL... Did you even try to do what I suggested? Attack this like you would any other dynamics problem: You identify the forces acting on each box. Draw a free body diagram for each. Then apply Newton's 2nd law.

This is what I don't understand: How to I add up the tension vectors to get a resultant tension in the rod?

You don't add up any tension vectors. The tension that the rod exerts on each box is one of the forces that will appear in your free body diagrams. Using Newton's 2nd law, you'll solve for that tension.

 

[KingKai]

Does it matter whether it is a rod between the two blocks or a string? This is what is tripping me up because with a string the masses can close together due the ability of a string to have slack, but with a rod the masses are held at a constant distance apart, is the difference in connection material of the two blocks negligible?

- KingKai

 

[howie8594]

For this problem it doesn't matter what the connection between the two blocks is because the upper block has a higher coefficient of friction than the lower one. This means it will be more resistant to the motion down the slope than the lower block will be. Therefore, the higher block would not slide into the lower one and the lower one only pulls on the higher one. No pushing force is necessary in this problem. Hope this makes sense.

 

[Doc Al]

Does it matter whether it is a rod between the two blocks or a string? This is what is tripping me up because with a string the masses can close together due the ability of a string to have slack, but with a rod the masses are held at a constant distance apart, is the difference in connection material of the two blocks negligible?

It's actually simpler with a rod, since that guarantees that the two boxes will have the same acceleration.