whatdoido
- 48
- 2
Hi, I'm having conceptual problems for solving this one.
1. Homework Statement
I drew a picture of this problem, which should show up below. Lengths x,a and b were given in the original picture.
A rotating closed cylinder is braked with a bar. Its brake shoe is pressed in respect of point B without friction. The bar AB presses the cylinder. Force F_1 is used in point A.
Calculate the needed force when cylinder stops from a rotational speed of 1200 RPM clockwise in 12 seconds. Cylinder's mass is 14 kg, radius 6,5 cm and frictional coefficient 0,33.
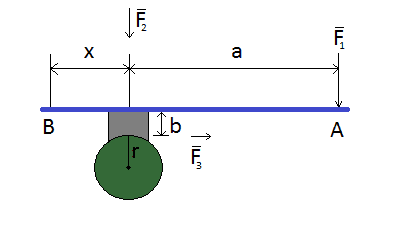
r=6,5 cm= 0,065m
\mu=0,33
x=7,0 cm=0,07m
a=19 cm=0,19m
b=1,2 cm=0,012m
m=14kg
\Delta t=12s
n=1200 RPM=20r/s
M=J\alpha
M=Fr
J=\frac{1}{2}mr^2
\sum M=0
Well I know how to calculate the force needed to stop the rotating cylinder
M=J\alpha\hspace{30mm}M=\mu Nr
J\alpha=\mu Nr
.
.
.
N=\frac{mr2\pi n}{t \mu}
=28,877... N
F_1 can be calculated with torques I'm pretty sure, but this is the spot where I am stuck at. Something like F_2 x=F_1 (x+a) won't do. I should somehow take in the consideration the clockwise movement of cylinder (in part b of this problem it is supposed to calculate F_1 in counter-clockwise movement). Cylinder has a torque F_3, right? So I thought that is what I am supposed to use, but I'm not sure how to proceed.. I tried using some angles and make it work, but I cannot think something that would make me think "oh of course! That's how I can solve it" and give me the correct answer, eventually.
1. Homework Statement
I drew a picture of this problem, which should show up below. Lengths x,a and b were given in the original picture.
A rotating closed cylinder is braked with a bar. Its brake shoe is pressed in respect of point B without friction. The bar AB presses the cylinder. Force F_1 is used in point A.
Calculate the needed force when cylinder stops from a rotational speed of 1200 RPM clockwise in 12 seconds. Cylinder's mass is 14 kg, radius 6,5 cm and frictional coefficient 0,33.
r=6,5 cm= 0,065m
\mu=0,33
x=7,0 cm=0,07m
a=19 cm=0,19m
b=1,2 cm=0,012m
m=14kg
\Delta t=12s
n=1200 RPM=20r/s
Homework Equations
M=J\alpha
M=Fr
J=\frac{1}{2}mr^2
\sum M=0
The Attempt at a Solution
Well I know how to calculate the force needed to stop the rotating cylinder
M=J\alpha\hspace{30mm}M=\mu Nr
J\alpha=\mu Nr
.
.
.
N=\frac{mr2\pi n}{t \mu}
=28,877... N
F_1 can be calculated with torques I'm pretty sure, but this is the spot where I am stuck at. Something like F_2 x=F_1 (x+a) won't do. I should somehow take in the consideration the clockwise movement of cylinder (in part b of this problem it is supposed to calculate F_1 in counter-clockwise movement). Cylinder has a torque F_3, right? So I thought that is what I am supposed to use, but I'm not sure how to proceed.. I tried using some angles and make it work, but I cannot think something that would make me think "oh of course! That's how I can solve it" and give me the correct answer, eventually.