Force of magnetic attraction between hemispheres

[Pouyan]

Homework Statement

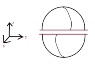
Calculate the force of magnetic attraction between the northern and southern hemispheres of a uniformly charged spinning spherical shell, with radius R, angular velocity ω and surface charge density σ.

Homework Equations

Maxwell Tensor : T_m = [/B](1/μ) * ((B*n)B - (1/2)*B² n)

B_in = (2/3)*μσRω*z
B_out = μm/(4πr³) * (2cosθ r + sinθ θ)
where m = (4/3)*πR³(σωR)

The Attempt at a Solution

I do see in my solution that :
1-We use a surface consisting of the entire equatorial plane, CLOSING IT with a hemispherical surface at infinity where (since the field is zero out there) contribution is zero.
for r>R :
B = μm/(4πr³) θ = - μm/(4πr³) z (Why ?! )
2- We have a equatorial circular disk. We use B inside and da = rdrdφ. Direction is in z-axis!
I don't want the solution because I already have it but MY QUESTIONS are :

A) How should think and imagine this spheres ?!
Should I think like this and use those formulas :

B) Why we do write B = μm/(4πr³) θ = - μm/(4πr³) z
Why is θ =-z in this case ?! I don't get it !
I know the rest. That is just integrating

 

[TSny]

A) How should think and imagine this spheres ?!
Should I think like this and use those formulas :

I'm not quite following what you are asking here. Can you reword the question?

B) Why we do write B = μm/(4πr³) θ = - μm/(4πr³) z
Why is θ =-z in this case ?! I don't get it !

It is because you are using spherical coordinates with θ measured from the positive z axis. The unit vector θ points in the direction of increasing θ. For a point on the equatorial plane of the sphere, what is the direction of θ?

 

[Pouyan]

I'm not quite following what you are asking here. Can you reword the question?



It is because you are using spherical coordinates with θ measured from the positive z axis. The unit vector θ points in the direction of increasing θ. For a point on the equatorial plane of the sphere, what is the direction of θ?

I've got it !

Thanks