Forces acting on a half circle by a standstill wire

[AndersB87]

Hello

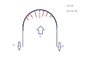
I have a problem where a wire is pulled around a half circle (disc) and then both ends pulled. The force in both ends are equal (F1 + F2).

The disc must in total put up a force (F3) equal to F1 + F2 to not be pulled along by the wire.


My question is how does the force of the wire act on the disc at different places. What is the force subjected to the disc from the wire at the top of the disc? as an example. Or at 45 degrees on each side?

I uploaded a picture of the problem, where the red lines indicates which individual forces I want to be able to calculated.

There is no movement to the wire.

 

[mfb]

The shortcut, and neglecting the mass of the wire: the vertical load is spread evenly over the vertical coordinate. Based on this, you can determine the force per length at the top of the cylinder (where there is no horizontal component). That value is the same everywhere on the half circle.

The long way: Split the half circle in triangles, calculate the force equilibrium for a triangle, let the triangle size go to zero.

 

[AndersB87]

Hello, thank you for the answer. I tried another approach to the problem where i looked at it as a boat submerged in water. The theory is that the largest forces is on the top of the circle, as a boat would experience the largest force at the bottom of the hull. The following link was very helpful.

http://www.engin.brown.edu/courses/en3/notes/Statics/forcesum/forcesum.htm


For a more general case I wrote the Force per length as an vector in the xy-plane, where the i-vector is x directon, and j-vector is y direction.

I found the general forumla for the force per angle to be:

dF/dPhi = F*(2/pi)*cos phi*(j*cos phi - i*sin phi)

Now I could just integrate this at the angles of interest to find the forces acting on the disc.

I wonder this approach is correct?