- #1
praskatonik
- 1
- 0
Hi.
I've been working on a project of angle stabilization for a vehicle moving along a string, looking like this:
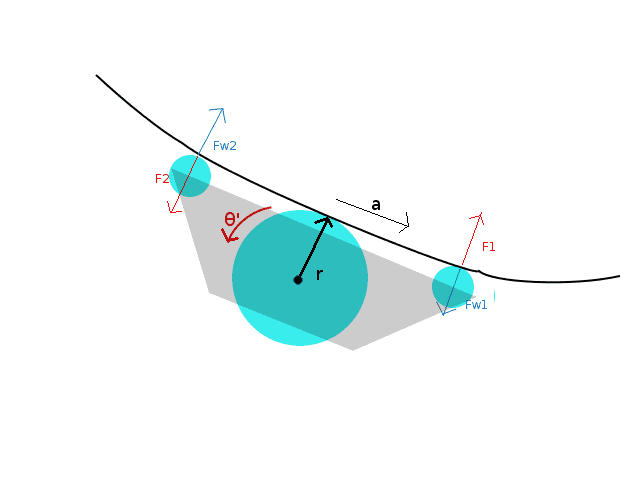
The propulsion system is connected to the central wheel, while the outer two wheels are used for support.
I've observed that during acceleration the vehicle rotates. I would estimate that this angle is proportional to the translational acceleration, and I need a way to quantify (or refute) my estimate.
My model is following:
τ - torque force generated by the propulsion
a - translational acceleration (αr = a)
r - radius of the driving wheel
F1, F2 - tangenial forces of chasis torque due to motor torque
Fw1, Fw2 - forces by which the wire opposes the deformation that the chasis torque would cause
θ' - angle velocity of the driving wheel
Is it correct to say that the following equation holds:
I*θ'' = τ - r*m*a
where I is the inertial moment of the chasis, and θ'' angle acceleration?
How to I model the tangenial forces of torque acting on the end-points of my chasis and the forces of deformation opposition exhibited by the wire?
I presume if it were a perfect, unbendable wire, it would be true that:
F1 = -Fw1 and
F2 = -Fw2
and no chasis rotation would be possible.
In my case, as in any real case of object hanging on a wire, this is not true.
Thank you all :)
Ana
P.S. This is my first dabble in anything rotational, so excuse my ignorance. This is how far I can get by using brain+Google.
I've been working on a project of angle stabilization for a vehicle moving along a string, looking like this:
The propulsion system is connected to the central wheel, while the outer two wheels are used for support.
I've observed that during acceleration the vehicle rotates. I would estimate that this angle is proportional to the translational acceleration, and I need a way to quantify (or refute) my estimate.
My model is following:
τ - torque force generated by the propulsion
a - translational acceleration (αr = a)
r - radius of the driving wheel
F1, F2 - tangenial forces of chasis torque due to motor torque
Fw1, Fw2 - forces by which the wire opposes the deformation that the chasis torque would cause
θ' - angle velocity of the driving wheel
Is it correct to say that the following equation holds:
I*θ'' = τ - r*m*a
where I is the inertial moment of the chasis, and θ'' angle acceleration?
How to I model the tangenial forces of torque acting on the end-points of my chasis and the forces of deformation opposition exhibited by the wire?
I presume if it were a perfect, unbendable wire, it would be true that:
F1 = -Fw1 and
F2 = -Fw2
and no chasis rotation would be possible.
In my case, as in any real case of object hanging on a wire, this is not true.
Thank you all :)
Ana
P.S. This is my first dabble in anything rotational, so excuse my ignorance. This is how far I can get by using brain+Google.