Theexploer
- 7
- 2
Thread moved from the technical forums to the schoolwork forums
TL;DR Summary: An accelerator pedal is located steadily on our line at point O, the spring AB is perpendicular to the accelerator pedal, keeping it balanced at an angle of 45 degrees. a = 45* the weight of the accelerator pedal is 10N and it is loaded on G. OG = 10 cm OB = 15 cm.
Question = Calculate the intensity of the force T applies to the accelerator pedal.
Question = Determine the direction, side, and density of R from point O.
For the firtst question i did like that =
As the pedal is in balance the sum of the moment of
external forces are zero
M(P)+M(T)+M(R)=0
M(R)=0 because it meets the axis of rotation
So M(P)+M(T)=0
If we choose a positive direction towards P
M(P)=P.dp or dp = OG.cosalpha=OGcos45°
M(T)=-T.OB
T=OGxcos45°xP/OB=10x10xcos45°/15
T=4.7N
But i'm not sure sor i can't do the second one.
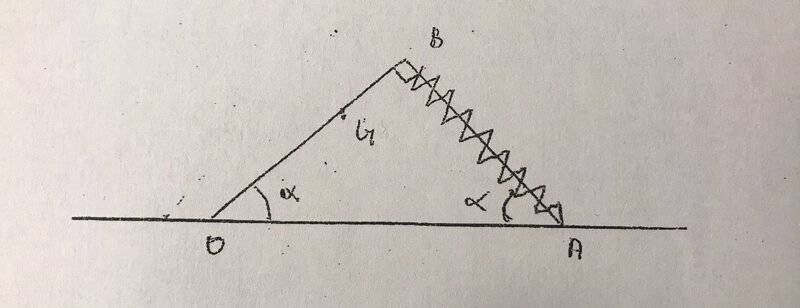
Question = Calculate the intensity of the force T applies to the accelerator pedal.
Question = Determine the direction, side, and density of R from point O.
For the firtst question i did like that =
As the pedal is in balance the sum of the moment of
external forces are zero
M(P)+M(T)+M(R)=0
M(R)=0 because it meets the axis of rotation
So M(P)+M(T)=0
If we choose a positive direction towards P
M(P)=P.dp or dp = OG.cosalpha=OGcos45°
M(T)=-T.OB
T=OGxcos45°xP/OB=10x10xcos45°/15
T=4.7N
But i'm not sure sor i can't do the second one.
 ##\qquad## !
##\qquad## !