Fortran Troubleshooting - Get Help with Codeblocks Issues

[felipearcaro]

I'm almost finishing this program, there is only one problem and i think it's because the complex numbers.
When i run the program and plot the graph (with Origin), appears:

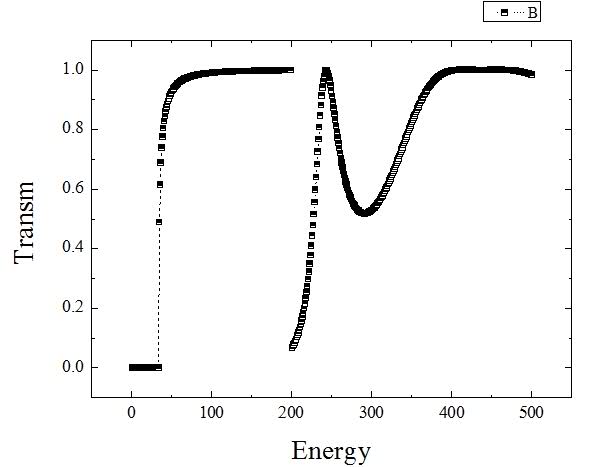
But the correct is:

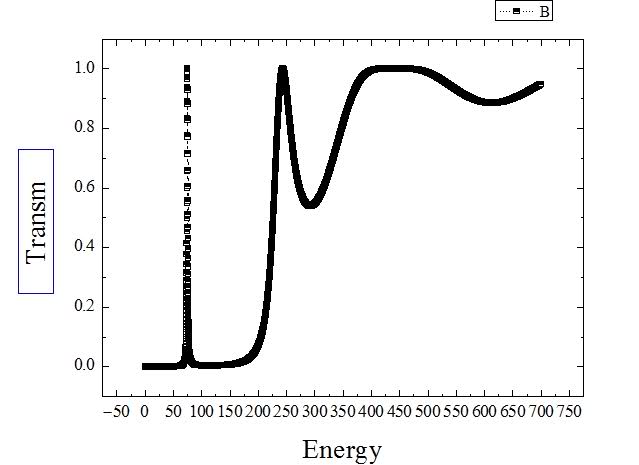
The part with the complex numbers (where V>E(K)) is the problem i think, because when E>200, it works fine.

      PROGRAM ABCDE


      IMPLICIT REAL (8) (A-B,D-H,O-Z) !Define numeros reais e imaginarios
      IMPLICIT COMPLEX (8)(C)
      PARAMETER(NZ=501, L=2) !Define parametros
      DIMENSION Z(NZ), X(NZ), Y(NZ), V(NZ), D1(L,L), P(L,L), D(L,L), I(NZ)
      DIMENSION Q(L,L), E(NZ)
      COMPLEX (8) CW(NZ), CKP(L,L), CKJ (L,L), CX(NZ), CY(NZ)
!
      OPEN(UNIT=12,FILE='VALORES2.DAT',FORM='FORMATTED')
      OPEN(UNIT=13,FILE='VALORES.DAT',FORM='FORMATTED')
      OPEN(UNIT=14,FILE='POT.DAT',FORM='FORMATTED')
      OPEN(UNIT=15,FILE='GRAPH.DAT',FORM='FORMATTED')
!
!
307   FORMAT(86(2X,E14.7))
308   FORMAT(I5,86(2X,E14.7))
       AM = 0.067D0 !Massa efetiva do e- (GaAs)
       EPS = 12.5D0 !Constante dielétrica (GaAs)
       RY = 13.6058D3 * AM / EPS / EPS
       A0 = 0.5292D0 * EPS / AM
       PI = 4.D0 * DATAN(1.D0)
       CZ = (0.D0,1.D0) !Unidade complexa

      !WRITE(*,*)'INSIRA ENERGIA DA PARTICULA INCIDENTE (meV)=' !Entrada da energia da particula incidente
      !READ(*,*) E1
      !E = E1/RY

      WRITE(*,*)'INSIRA O COMPRIMENTO=' !Entrada do comprimento avaliado
      READ(*,*) ALF
      AL = ALF/A0


      DZ = AL/(NZ-1)

      CALL MESH(AL,DZ,Z) !Chama subrotina que fraciona o comprimento (em pedacos de tamanho dz)
      CALL POTE(A0,RY,AL,Z,V) !Chama subrotina que define o potencial em todo o comprimento

    !DO M=1,NZ
    !E(M)=M
    !WRITE(*,*) E(M)
    !ENDDO


      DO K=1,NZ !L=E1, pois a variavel precisava ser inteiro
      E(K)=K/RY

      CKB = DSQRT(E(K)-V(1))

      DO M=1,NZ

      IF (E(K).GT.V(M+1)) THEN
      AK2 = DSQRT(E(K)-V(M+1))
      CDM = AK2/CKB
      CKZ = CDEXP(CZ*CKB*DZ)
      CKB = AK2

      !WRITE(*,*) CK2

      ELSE
      CK2 = DSQRT(V(M+1)-E(K))*CZ
      CDM = CK2/CKB
      CKZ = CDEXP(CZ*CKB*DZ)
      CKB = CK2

      ENDIF
      !WRITE(*,*) CK2


      !WRITE(*,*) CMD

      !WRITE(*,*)  CKZ

      CW(M) = CKZ
      !WRITE(*,*)CW(M)
      CX(M) = (1.D0 + CDM)/2.D0
      !WRITE(*,*) CX(M)
      CY(M) = (1.D0 - CDM)/2.D0
      !WRITE(*,*) CY(M)



      ENDDO

      !WRITE(*,*) CKB, V(2)*RY, E



      !D1 (1,1) = X(1)
      !D1 (2,1) = Y(1)
      !D1 (1,2) = Y(1)
      !D1 (2,2) = X(1)

      CALL CALCM(CX,CY,CW,CKJ)

      CKT11= CX(1)*CKJ(1,1)+CY(1)*CKJ(2,1)

      !CKT(1,2)
      CKT21 = CY(1)*CKJ(1,1)+CX(1)*CKJ(2,1)
      !WRITE(*,*) CKT21
      !CKT(2,2)

      !CKY(1,1,M) = D(1,1)*CP(1,1)+D(1,2)*P(2,1)
      !KY(1,2,M) = D(1,1)*P(1,2)+D(1,2)*P(2,2)
      !KY(2,1,M) = D(2,1)*P(1,1)+D(2,2)*P(2,1)
      !KY(2,2,M) = D(2,1)*P(1,2)+D(2,2)*P(2,2)

      !CKT(2,1) = CT1
      !CKT(1,1) = CT2


      !Define a eficiencia
      ACF = 1.D0 - (CDABS(CKT21))**2/(CDABS(CKT11))**2
      !WRITE(*,*) CDABS(CKT21), CDABS(CKT11)


      WRITE (15,307) E(K)*RY, ACF
      ENDDO


      END PROGRAM ABCDE


!@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@

      SUBROUTINE CALCM(CX,CY,CW,CKJ)

!@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
!
      IMPLICIT REAL (8) (A-B,D-H,O-Z) !Define numeros reais e imaginarios
      IMPLICIT COMPLEX (8)(C)
      PARAMETER(NZ=501, L=2)
      DIMENSION Z(NZ), V(NZ)
      !DIMENSION
      COMPLEX (8) CX(NZ), CY(NZ), CW(NZ), CKW(L,L), CKJ (L,L), CKY(L,L,NZ)


      !Faz D*P para todos as barreiras D2*P2, D3*P3..
      DO M = 1,NZ
       CKY(1,1,M) = DCONJG(CW(M))*CX(M)
       CKY(1,2,M) = DCONJG(CW(M))*CY(M)
       CKY(2,1,M) = CW(M)*CY(M)
       CKY(2,2,M) = CW(M)*CX(M)
       !WRITE(*,*) DCONJG(CW(M))

      ENDDO
      !Faz a primeira multiplicação para o loop [D2*P2].[D3*P3]
      CKW(1,1) = CKY(1,1,2)*CKY(1,1,3) + CKY(1,2,2)*CKY(2,1,3)
      CKW(1,2) = CKY(1,1,2)*CKY(1,2,3) + CKY(1,2,2)*CKY(2,2,3)
      CKW(2,1) = CKY(2,1,2)*CKY(1,1,3) + CKY(2,2,2)*CKY(2,1,3)
      CKW(2,2) = CKY(2,1,2)*CKY(1,2,3) + CKY(2,2,2)*CKY(2,2,3)
      !WRITE(*,*) CKW(1,1)

      !Faz o resto das mutiplicações usando o resultado da ultima como um fator a multiplicar
      DO M = 4,NZ
       CKJ(1,1) = CKW(1,1)*CKY(1,1,M) + CKW(1,2)*CKY(2,1,M)
       CKJ(1,2) = CKW(1,1)*CKY(1,2,M) + CKW(1,2)*CKY(2,2,M)
       CKJ(2,1) = CKW(2,1)*CKY(1,1,M) + CKW(2,2)*CKY(2,1,M)
       CKJ(2,2) = CKW(2,1)*CKY(1,2,M) + CKW(2,2)*CKY(2,2,M)

       !Renova o valor do fator a mutiplicar
       CKW(1,1) = CKJ(1,1)
       CKW(1,2) = CKJ(1,2)
       CKW(2,1) = CKJ(2,1)
       CKW(2,2) = CKJ(2,2)
    !WRITE(*,*) CKW(1,1)
      ENDDO


      RETURN
      END  SUBROUTINE CALCM

!@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
!
      SUBROUTINE MESH(AL,DZ,Z)

!@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
!
      IMPLICIT REAL(8) (A-H,O-Z)
      PARAMETER (NZ=501)
      DIMENSION Z(NZ)
!

      DO I=1,NZ
      Z(I) = DFLOAT(I-1) * DZ
      ENDDO
 !
      RETURN
      END  SUBROUTINE MESH

!@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@

      SUBROUTINE POTE(A0,RY,AL,Z,V) !**********

!@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@

      IMPLICIT REAL(8) (A-H,O-Z)
      PARAMETER (NZ=501)
      DIMENSION Z(NZ), V(NZ)

        ALH = 0.5D0 * AL  !MEIO DO SISTEMA
        DQW = 50.D0 / A0   ! DISTANCIA ENTRE POCOS
        DQWH = 0.5D0 * DQW
        QW = 50.D0 / A0   ! LARGURA DOS POCOS
        QWH = 0.5D0 * QW
        AT = DQWH + QW

        DO IZ=1,NZ
        ZW = Z(IZ) - ALH
        V(IZ) = 0.D0
        IF(DABS(ZW).GT.DQWH.AND.DABS(ZW).LT.AT)  V(IZ) = 200.D0/RY
        WRITE(14,*) Z(IZ)*A0, V(IZ)*RY
        ENDDO
 !
      RETURN
      END  SUBROUTINE POTE

 

[felipearcaro]

I think the problem is in this part ELSE
CK2 = DSQRT(V(M+1)-E(K))*CZ
CDM = CK2/CKB
CKZ = CDEXP(CZ*CKB*DZ)
CKB = CK2

 

[felipearcaro]

Anyone?