Fourier Series Convergence at the Origin

[robertjford80]

Homework Statement

The Attempt at a Solution

Obviously brackets mean something other than parentheses because .5[0 + 0] ≠ .5

 

[Mark44]

The brackets mean the same thing as parentheses...

I was unable to "Dirichlet's theorem" on the web, except as it applies to number theory and prime numbers. In Kreyszig's Advanced Engineering Mathematics, 3rd Ed., there is a theorem (identified only as Theorem 1) in the section titled "Fourier Series. Euler Formulas," and I believe that's the one you're mentioning.

If a periodic function f(x) with period $2\pi$ is piecewise continuous in the interval $-\pi \leq x \leq \pi$ and has a left-and right-hand derivative at each point of that interval, then the corresponding Fourier series (7) [with coefficients (6)] is convergent. Its sum is f(x), except at a point x₀ at which f(x) is discontinuous and the sum of the series is the average of the left- and right-hand limits of f(x) at x₀.

The numbers in parentheses are, respectively, the usual definition of a Fourier series, and the formulas for the coefficients of the series.

The theorem is talking more about the function represented by the Fourier series, and not so much about the function the series represents. At most points, the two are identical, but at discontinuities, they are different.

The theorem doesn't say that f($-\pi/2$) = 1/2. It says that the value of the series at x = $-\pi/2$ is 1/2.

 

[LCKurtz]

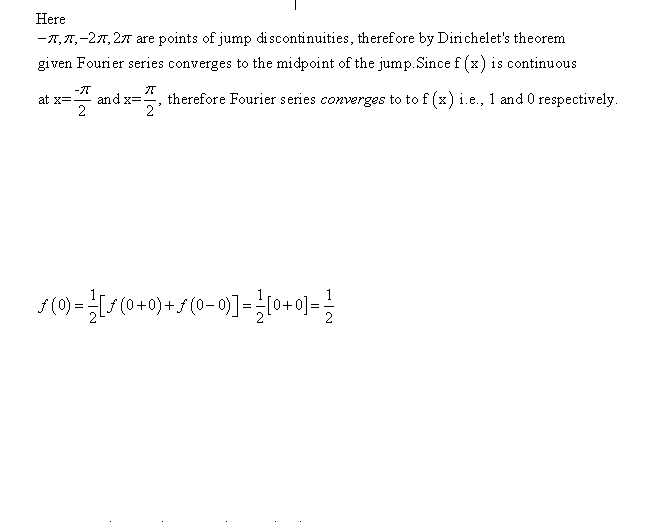
The Attempt at a Solution

Obviously brackets mean something other than parentheses because .5[0 + 0] ≠ .5

That's just a typo. It should read$$\frac 1 2[f(0^+)+f(0^-) =\frac 1 2 [0+1]=\frac 1 2$$and it isn't f(0); it is the value of the FS at 0.