Fourier series (maybe) of e^x from 0 to 2pi

[iceblits]

Hey,
I have to show:

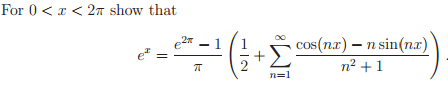
Should I try to find the Fourier series from -2pi to 2pi? I have tried this already but I can't seem to get rid of the cos(nx/2) and sin(nx/2) to turn them into just sin(nx) and cos(nx) and the denominator stays as (n^2+4 instead of n^2+1.

Any suggestions would be very helpful.

 

[SadScholar]

It's probably easiest to use the complex Fourier series.
$$
f(x)=e^x=\sum_{-\infty}^\infty C_n e^{in\pi x/\ell}\text{, where}\\
C_n=\frac{1}{2\ell}\int_{-\ell}^\ell f(x)e^{-in\pi x/\ell}\, \mathrm{d}x\text{.}
$$
The range of integration will be a little different in your case. You can picture $e^x$ as being a function that repeats every $2\pi$. Effectively, $\ell=\pi$, but you're not integrating symmetrically about the origin.
$$
C_n=\frac{1}{2\pi}\int_{0}^{2\pi} e^xe^{-in\pi x/\pi}\, \mathrm{d}x=\frac{1}{2\pi}\int_{0}^{2\pi}e^{(1-in)x}\, \mathrm{d}x\\
=\frac{1}{2\pi(1-in)}e^{(1-in)x}\big|_0^{2\pi}\\
=\frac{e^{2\pi}-1}{2\pi(1-in)}=C_n
$$
I should probably let you handle it from here. Use the expression given for $f(x)$ above.