- #1
Aziza
- 190
- 1
The Fourier series of a delta train is supposedly (1/T) + (2/T ) Ʃcos(nωt) ...
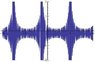
where T is period and ω=2*Pi/T ...but when I plot this, it doesn't give me just a spike towards positive infinity, but towards negative infinity as well (see attached pic), so this does not seem to converge to the delta function we want... ?
Also I am kindof confused as to how this is actually derived. The way my book does it is it starts with a backwards sawtooth wave. The derivative of this is a delta train, with the deltas going towards positive infinity...the Fourier series of this sawtooth wave is
f(t) = (1/2) + (2/T ) Ʃ(1/n)sin(nωt)
But f(t) can also be written as a generalized function:
f(t) = (1-(t/T)) + Ʃu(t-nT)
where u is the heavyside function
Taking derivative of first f(t) gives
f'(t) = (2/T ) Ʃcos(nωt) (1)
But taking derivative of second f(t) gives
f'(t) = -(1/T) + Ʃδ(t-nT) (2)
Ok I understand everything so far, but now my book says that equation (1) doesn't converge 'in the ordinary sense' but 'we can say that this series converges to the generalized function' given by equation (2)...huh? How can (1) converge to (2) if (1) gives a different graph than (2) ?? That is my first confusion.
Next the book just equates (1) and (2) and so gets the Fourier series for Ʃδ(t-nT)...but I am confused as to why we can just equate them if they are not really the same thing...
where T is period and ω=2*Pi/T ...but when I plot this, it doesn't give me just a spike towards positive infinity, but towards negative infinity as well (see attached pic), so this does not seem to converge to the delta function we want... ?
Also I am kindof confused as to how this is actually derived. The way my book does it is it starts with a backwards sawtooth wave. The derivative of this is a delta train, with the deltas going towards positive infinity...the Fourier series of this sawtooth wave is
f(t) = (1/2) + (2/T ) Ʃ(1/n)sin(nωt)
But f(t) can also be written as a generalized function:
f(t) = (1-(t/T)) + Ʃu(t-nT)
where u is the heavyside function
Taking derivative of first f(t) gives
f'(t) = (2/T ) Ʃcos(nωt) (1)
But taking derivative of second f(t) gives
f'(t) = -(1/T) + Ʃδ(t-nT) (2)
Ok I understand everything so far, but now my book says that equation (1) doesn't converge 'in the ordinary sense' but 'we can say that this series converges to the generalized function' given by equation (2)...huh? How can (1) converge to (2) if (1) gives a different graph than (2) ?? That is my first confusion.
Next the book just equates (1) and (2) and so gets the Fourier series for Ʃδ(t-nT)...but I am confused as to why we can just equate them if they are not really the same thing...