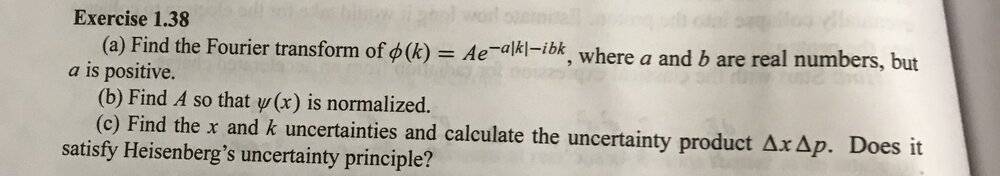SUMMARY
The discussion centers on using Mathematica for performing Fourier Transform and Inverse Fourier Transform. The user emphasizes the importance of defining a function in terms of the variable ##k## rather than ##x## to correctly compute the inverse Fourier transform to obtain ##f(x)##. Additionally, it is crucial to note that the variable ##b## should be multiplied by ##k##, not by the absolute value of ##k##, to ensure accurate results in the transformation process.
PREREQUISITES
- Understanding of Fourier Transform and Inverse Fourier Transform concepts
- Familiarity with Mathematica software and its syntax
- Knowledge of function definitions in mathematical terms
- Basic grasp of variable manipulation in mathematical equations
NEXT STEPS
- Explore Mathematica's documentation on Fourier Transform functions
- Learn how to define functions in Mathematica using the variable ##k##
- Study examples of Inverse Fourier Transform in Mathematica
- Investigate the implications of variable manipulation in Fourier analysis
USEFUL FOR
Students and professionals in mathematics, physics, and engineering who are working with Fourier Transforms in Mathematica, particularly those seeking to understand the nuances of variable definitions and transformations.