Fourier Transform - Solutions Error?

[flyusx]

Homework Statement

Calculate the Fourier series of $$\phi(k)=\sqrt{\frac{3}{2a^3}}(a-\vert k\vert)$$ for $\vert k\vert\leq a$, where $\phi(k)=0$ elsewhere.

Relevant Equations

$$\mathcal{F}=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\phi(k)\exp(ikx)\;dk$$

This is technically a Fourier transform of a quantum function, but the problem I'm having is solely mathematical.
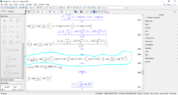
Conducting this integral is relatively straightforward. We can pull the square roots out since they are constants, rewrite the bounds of the integral to be from $-a$ to $a$ (since the function is zero outside this bound), split the integral into two parts to get rid of the absolute value of $k$ and do integration by parts. Prior to integration by parts, the Fourier transform becomes
$$\sqrt{\frac{3}{4\pi a^{3}}}\left(\int_{-a}^{0} k\exp(ikx)\;dk-\int_{0}^{a}k\exp(ikx)\;dk+a\int_{-a}^{a}\exp(ikx)\;dk\right)$$
I did integration by parts by hand and used Maple to convert the exponentials into trig. The Fourier transform simplifies into $$\sqrt{\frac{12}{\pi a^{3}}}\frac{1}{x^{2}}\sin^{2}\left(\frac{ax}{2}\right)$$.
However, the book (Zettili Quantum Mechanics, Problem 1.11a on page 75 of the 3rd edition, probably present in previous editions) says the Fourier transform is equal to $$\frac{4}{x^{2}}\sin^{2}\left(\frac{ax}{2}\right)$$. Seeing as Maple confirms my Fourier transform to be correct, I know I didn't make an error so is this an error in the book?

 

[anuttarasammyak]

For a<0 your solution gives pure imaginary. It diverges for a $\rightarrow$ 0, not zero. Is it OK?

 

[flyusx]

I'm not quite sure what happened to the question formatting or my answer. I must have copy/pasted the wrong thing. My apologies.

The correct problem statement should be to find the Fourier transform of
$$\sqrt{\frac{3}{2a^{3}}}(a-\vert k\vert), \vert k\vert\leq a$$

I've uploaded a corrected version for which Maple confirms my answer of $$\sqrt{\frac{3}{\pi a^{3}}}\frac{1-\cos(ax)}{x^{2}}$$ is valid. It also states that the answer is the book $$\frac{4}{x^{2}}\sin\left(\frac{ax}{2}\right)^{2}$$ is wrong.

 

[renormalize]

Can you post a scan of the page from your Zettili book reference so that we can read the actual problem as stated?

 

[vela]

I found the problem in my copy of the second edition of Zittili. It looks like they dropped the constant factor in front, but doing so doesn't affect the reasoning in the rest of the solution. The book just wanted to show you that the unnormalized wave function is of the form
$$\phi(x) = a^2 \left(\frac{\sin u}{u}\right)^2$$ where $u=ax/2$. An overall constant factor doesn't affect $\Delta x$, so the absence of the normalization constant doesn't really matter.

 

[anuttarasammyak]

The book just wanted to show you that the unnormalized wave function is of the form
ϕ(x)=a2(sin⁡uu)2 where u=ax/2. An overall constant factor doesn't affect Δx, so the absence of the normalization constant doesn't really matter.

In this setting $\phi(x)$ seems to have physical dimension of L^-2 though 1D wave function has that of L^-1/2 normally. It does not matter neither ? If the coefficient were $\sqrt{a}$, it would be OK , though I have no idea whether there exist other physical constants given in the problem.