kronoskar
- 3
- 0
Hi,
I have a question about basic statics.
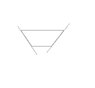
I have heard from someone that the forces acting on a truncated cone in a hole of corresponding geometry is different from an ordinary block sliding down a wedge, since the normal force on one side of the cone will be affected by the normal force on the other side. I've had some difficulties concerning this when trying to figure out the frictional forces occurring when the cone is turned/screwed/pressed downards into the hole. I've attached a jpg showing a truncated cone wedged into a hole of a corresponding geometry (drawing in 2D but problem probably to be solved in 3D), the cone is symmetrical.
That is, will the normal force on each side of the cone be larger than each of the horisontal force (for example mg)?
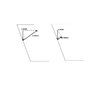
For block sliding down a wedge, the relation between the normal force and the horisontal force is something like this:
http://i359.photobucket.com/albums/oo31/tanzl/freebodydiagram1.jpg
Would gladly appreciate the help!
Brgd
Oskar
I have a question about basic statics.
I have heard from someone that the forces acting on a truncated cone in a hole of corresponding geometry is different from an ordinary block sliding down a wedge, since the normal force on one side of the cone will be affected by the normal force on the other side. I've had some difficulties concerning this when trying to figure out the frictional forces occurring when the cone is turned/screwed/pressed downards into the hole. I've attached a jpg showing a truncated cone wedged into a hole of a corresponding geometry (drawing in 2D but problem probably to be solved in 3D), the cone is symmetrical.
That is, will the normal force on each side of the cone be larger than each of the horisontal force (for example mg)?
For block sliding down a wedge, the relation between the normal force and the horisontal force is something like this:
http://i359.photobucket.com/albums/oo31/tanzl/freebodydiagram1.jpg
Would gladly appreciate the help!
Brgd
Oskar