How Does Wind Affect the Forces on a Hanging Spider?

[DB]

a small spider weighing about 6.0e-3 N, hangs on its thread from the branch of a tree. A horizontal wind blows the spider and the thread to and angle of 35 degrees from the vertical.
a)find the horizontal force of the wind on the spider
b)find the tension in the thread

i got a, here's wat i did..

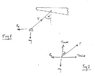
i drew a free body diagram
first i made the x-axis the tensile force in the thread, so in that case, the horizontal force was -35 degrees from the x-axis and the gravitational force was -35 degrees from the y axis. knowing that the spider is in dynamic equilibrium, i resolved the components of F_h and F_g

so i knew that to solve for F_h i had to get at least 1 of the x',y' components of F_h and use trig to solve for the hypotneuse, i knew this because the net force on the spider has to be 0.

so:
0.006sin(35)=\sim 0.00344

that gave me the x' component of F_h, so then the hypotneuse is

\frac{0.00344}{sin35}=\sim 0.0042

so the force of the wind on the spider would have to be about 0.0042 N, which the answer book says is right.

b) here i don't know wat to do, i know wat tension is, but my teacher hasnt showed me how to do this, and its not in the book. i thought that the sum of F_h and F_g would give me F_t but that's not it, the answer 7.3e-3 N and i don't know how to get there, some help would be apreciated :)

 

[Fermat]

Why not resolve the tension into two components at right angles to each other.

One component in the (opposite) direction of the wind force and the other component in the (opposite) direction of the weight of the spider.

 

[DB]

okay, but wat about finding the tension, how do i do that?

 

[Fermat]

okay, but wat about finding the tension, how do i do that?

If T is the tension then Tcos@ = mg, Tsin@ = F (the wind force)
Square the eqns and add them

 

[DB]

thanks fermat, but i don't understand wat u did...

 

[Fermat]

OK, I'll draw a diagram, and we'll see if that helps. Back shortly.

 

[Fermat]

In Fig1, you can see that there are three forces acting on the spider. Its own weight, mg, the force of the wind, Fw, and the tension in the string, T.
The string is at an angle of @=35 to the vertical.
In Fig2, I have resolved the Tension into horizontal and vertical components, Tsin@ and Tcos@ respectively.
The spider is in equilibrium so the Forces are all balanced with each other.

Vertical forces
Tcos@ = mg

Horizontal forces
Tsin@ = Fw

Squaring the eqns gives,

T²cos²@ = m²g²
T²sin²@ = Fw²

adding these eqns together,

T²(cos²@ + sin²@) = m²g² + Fw²
T² = m²g² + Fw²
=============
http://img314.imageshack.us/img314/7643/db4co.th.jpg

 

[Fermat]

Hmm, The attachment isn't showing. I'll use imageshack. Take a few more minutes.

 

[DB]

thanks for the diagram i really apreciate it, i got the right answer now, but not exactly in your way. once i saw how u resolved the tensile force, i just did Tsin(35)=4.2e-3, and Tcos(35)=6.0e-3, solving those gave me the x and y components to the tensile force (they were both equal so i didnt even have to use pythagorus) and it gave me, 7.3e-3 N which is the right answer, thanks