Phazall
- 2
- 0
1. Problem Statement
Transform equation 1 into equation 2 to show they're equivalent.
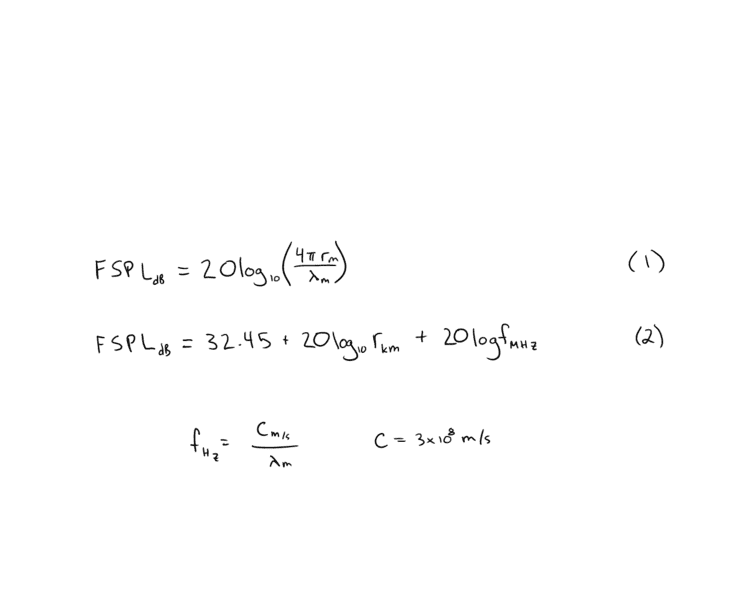
*Please note that I added a subscript to each variable indicating the units.
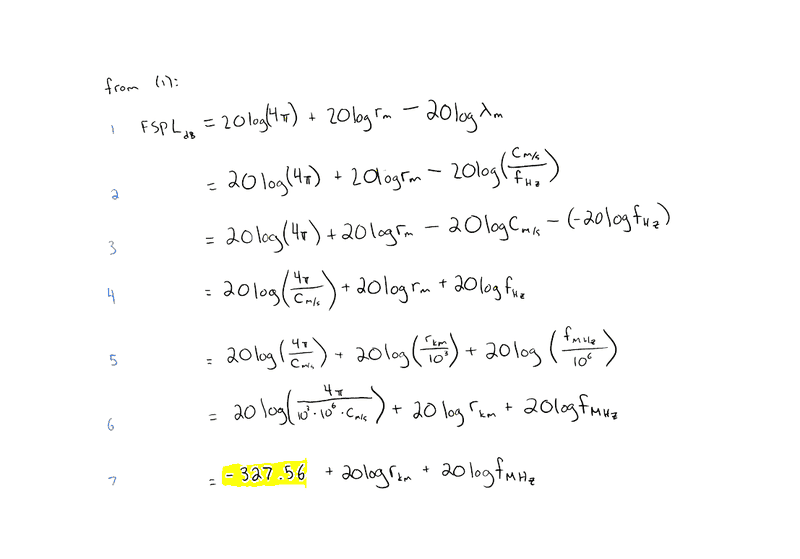
The highlighted constant shown in my attempt at the solution is supposed to be 32.45 according to both my notes and wikipedia http://en.wikipedia.org/wiki/Free-space_path_loss.
Thank you very much!
Transform equation 1 into equation 2 to show they're equivalent.
Homework Equations
*Please note that I added a subscript to each variable indicating the units.
The Attempt at a Solution
The highlighted constant shown in my attempt at the solution is supposed to be 32.45 according to both my notes and wikipedia http://en.wikipedia.org/wiki/Free-space_path_loss.
Thank you very much!